Из Опыта известно что сопротивление R цилиндрического проводника длиною l и площадью поперечного сечения S:
 ρ
ρ 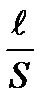 S,
S, 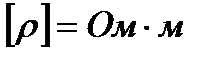

ρ = ρ  (1+αtoC), I=
(1+αtoC), I=  , I=
, I=  ∙
∙  ∙S │:S,
∙S │:S,  =
=  ∙
∙ 
Это эквивалентно выражению: ј =σE
 - это закон Ома в диф.форме; если присутствуют сторонние силы:
- это закон Ома в диф.форме; если присутствуют сторонние силы: 
Закон Джоуля-Ленца (1841-1842)
При прохождении заряда q по участку цепи I=q/t, q=It, совершается работа A=qU=IUt
Если проводник неподвижный и отсуствует хим.реакции, то работа А идёт на увеличение внутренней энергии проводника: Q=IUt. Чаще в такой форме Q=  Rt.
Rt.
Если ток переменный I=I(t): dQ=  (t)Rt, Q=
(t)Rt, Q= 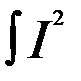 (t)Rdt
(t)Rdt
Получим теперь закон в диф.форме(локальной форме): Объёмной плотностью тепловой мощности называется тепловая энергия в единице объёма за единицу времени: 
Поскольку Q=IUt то получим: ω =  =
=  = јE
= јE
 – закон Джоуля-Ленца в диф.форме
– закон Джоуля-Ленца в диф.форме
ω=σ  ,т.к E=ј/σ, ω= ρ
,т.к E=ј/σ, ω= ρ 
18. Правило Киргоффа расчёта разветвлённых электр.цепей.
Рассмотрим электр. цепь. 
А и В - узлом называется точка в которой сходятся 3 и более проводника.
1 правило Кирхгоффа: «алгебр сумма токов сход в узле = 0»
 =0
=0
 ток I входящий в узел счит «+»,вых «-».
ток I входящий в узел счит «+»,вых «-».
узел A: I1-I2-I=0 (1), узел B:-I1-I2+I=0 (2)
2 правило Кирхгоффа: «алгебр сумма произв сил токов на сопротивление соотв уч контура = алгебр сумме ЕДС в рассм контуре»:  =
=  При этом выбирают определённое направление обхода контура, если направление тока совпадает с направлением обхода контура то его считают положительным. ЭДС считают + если при выбранном направлении ток проходит от – к +. При этом число независимых уравнений получается меньше чем общее число контуров.
При этом выбирают определённое направление обхода контура, если направление тока совпадает с направлением обхода контура то его считают положительным. ЭДС считают + если при выбранном направлении ток проходит от – к +. При этом число независимых уравнений получается меньше чем общее число контуров.
r 1  1R1: I1r1+IR=
1R1: I1r1+IR=  1 (3)
1 (3)
 1 r 1
1 r 1  2 r 2:I1r1-I2r2=
2 r 2:I1r1-I2r2=  1-
1-  2 (4)
2 (4)
R  2 r 2:I2 r2+IR=
2 r 2:I2 r2+IR=  2 (5)
2 (5)
(4)+(5) 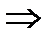 3. (1) (3) (4) позволяют найти токи I1 I2 I
3. (1) (3) (4) позволяют найти токи I1 I2 I

20. Закон Ома в классической электронной теории
Основные положения классической электронной теории Mе:
1) в Mе имеющих поликристаллическую структуру имеются свободные электроны: электроны положительности, электронный газ;
2) электроны участвуют в упорядоченном и хаотическом движениях. Упорядоченные движения описываются механикой Ньютона: F=ma
3) хаотическое движение электрона описывается моделью идеального газа, подчиняющегося классической статистике Максвелла-Больцмана.
4) между кристаллической решеткой Ме и электронами проводимости устанавливается тепловое равновесие.
 Получим дифференциальную форму закона Ома из электронной связи:
Получим дифференциальную форму закона Ома из электронной связи:
плотность j связана с концентрацией электронов n, зарядом e, скоростью упорядоченного движения <v> соотношением:
 j=en<v>, I=q/t=enV/t=enSl/t=enSv, I/S=env, j=en<v>
j=en<v>, I=q/t=enV/t=enSl/t=enSv, I/S=env, j=en<v>
Пусть «е» при соудар с узлом кристаллической решетки полностью передает всю энергию решетке и нач движение с vo=0. Под действ эл-кого поля с напряженностью E на «е» будет действ сила: F=eE. Тогда «е» приобретает ускорение: a=F/m=eE/m. Мax скорость электрона в конце свободного пробега будет равна: vmax=a<τ>; <τ> - среднее время свободного пробега. vmax=eE/m<τ>. Т.к. движение электрона равноускоренное, то скорость электрона равна:  . Ср время свободного пробега <τ> равно отношению ср длины св проб <l> к ср скор хаотического движения электронов <u>: <τ> =<l>/<u>. <v>=eE<l>/2m<u>. В этом случае мы пренебрегаем скоростью упорядоченного движения электронов в сравнении со скоростью хаотического, теплового движения электронов: <u> >> <v>: Т обр пол: j=e·n·e·E<l>/2m<u>=δE; δ=e2n<l>/2m<u> - электропроводность (j= δE). Если бы «е» не сталкивались с узлами решетки, то ср длина своб пробега l=∞ и электропроводность δ=∞ и не было бы эл-кого сопротивления. Тогда электрическое сопротивление мет в классической электронной теории вызвано столкновением свободных электронов с ионами решетки. По классической теории удельное сопротивление ρ=1/δ пропорционально средней скорости теплового движения <u>: <u>=√(8kT/2m)~√T. из опыта вытекает, что ρ=ρо(1+αT)
. Ср время свободного пробега <τ> равно отношению ср длины св проб <l> к ср скор хаотического движения электронов <u>: <τ> =<l>/<u>. <v>=eE<l>/2m<u>. В этом случае мы пренебрегаем скоростью упорядоченного движения электронов в сравнении со скоростью хаотического, теплового движения электронов: <u> >> <v>: Т обр пол: j=e·n·e·E<l>/2m<u>=δE; δ=e2n<l>/2m<u> - электропроводность (j= δE). Если бы «е» не сталкивались с узлами решетки, то ср длина своб пробега l=∞ и электропроводность δ=∞ и не было бы эл-кого сопротивления. Тогда электрическое сопротивление мет в классической электронной теории вызвано столкновением свободных электронов с ионами решетки. По классической теории удельное сопротивление ρ=1/δ пропорционально средней скорости теплового движения <u>: <u>=√(8kT/2m)~√T. из опыта вытекает, что ρ=ρо(1+αT)
Классическая электронная теория расходится с опытом потому, что:
1) движение электронов в Ме описывается не II законом Ньютона, а уровнением квантовой механики Шредингера;
2) поведение эл. газа подчиняется не классической теории Максвелла-Больцмана, а Ферми- Дирака;
3) при низких температурах взаимодействие между электронами доминирует над взаимодействием между электронами и решеткой.
В квантовой механике электроны проявляют волновые свойства и тогда сопротивление Ме обусловлено рассеиваньем электронных волн на квантах колебаний узлов кристаллической решетки – фононах.
21. Сила Ампера. Вектор магнитной индукции


 Оп путем было устан, что движущиеся эл-кие заряды, т. е. токи создают магнитные поля. Магнитное поле проявляется под действием сил магнитного взаимодействия. Магнитное поле в отличие от эл-кого действует только на движ заряды, на покоящиеся заряды не действует. (монополь – магнитный заряд) Сп-сть магнитного поля вызывать мех силу в каждой точке поля, действ на элемент тока Id(в-р)l хар-тся магнитной индукцией (вектор) B. Эл-т тока Id(в-р)l есть произв силы тока I на беск малый отрезок проводника d(в-р)l, направл по току. dI(в-р)l играет роль пробного заряда в электростатике. Ампер эксп-но установил, что сила d(в-р)F действ на элемент тока Id(в-р)l с индукцией (в-р) B равна:
Оп путем было устан, что движущиеся эл-кие заряды, т. е. токи создают магнитные поля. Магнитное поле проявляется под действием сил магнитного взаимодействия. Магнитное поле в отличие от эл-кого действует только на движ заряды, на покоящиеся заряды не действует. (монополь – магнитный заряд) Сп-сть магнитного поля вызывать мех силу в каждой точке поля, действ на элемент тока Id(в-р)l хар-тся магнитной индукцией (вектор) B. Эл-т тока Id(в-р)l есть произв силы тока I на беск малый отрезок проводника d(в-р)l, направл по току. dI(в-р)l играет роль пробного заряда в электростатике. Ампер эксп-но установил, что сила d(в-р)F действ на элемент тока Id(в-р)l с индукцией (в-р) B равна:  – закон Ампера (сила Ампера). Если проводник прямолинейный и магнитное поле однородное (одинаковое в каждой точке), интегрируя последнее выражение, получаем:
– закон Ампера (сила Ампера). Если проводник прямолинейный и магнитное поле однородное (одинаковое в каждой точке), интегрируя последнее выражение, получаем:  . Направление силы Ампера (в-р)F опр по правилу в-рного произведения. Сила (в-р)F ┴-а пл-сти, в кот лежат в-ры l и B и напр силы (в-р)F опред правилом правого винта: «если рукоятка правого винта вращается от первого вектора l ко второму ве-ру B на кратчайший угол, то поступательное движ винта указ направление силы (в-р)F». Модуль силы Ампера:
. Направление силы Ампера (в-р)F опр по правилу в-рного произведения. Сила (в-р)F ┴-а пл-сти, в кот лежат в-ры l и B и напр силы (в-р)F опред правилом правого винта: «если рукоятка правого винта вращается от первого вектора l ко второму ве-ру B на кратчайший угол, то поступательное движ винта указ направление силы (в-р)F». Модуль силы Ампера:  . Сила Ампера нецентральная, т. е. зависит от ориентации проводника с током в магнитном поле. Из з-на Ампера обычно определяют магнитную индукцию (в-р) B. Пусть проводник прямолинейный и ┴-ый однородному магнитному полю (в-р) B: F=IlB, B=F/Il. Магнитная индукция (вектор) B – силовая, в-ная хар-ка магнитного поля, числ равная силе, действ- со стороны однородного магнитного поля на единицу длины проводника, по которому течет ток =1А и расположение проводника ┴-о напр магнитного поля. Ед изм В в системе СИ явл Тесла (Тл). 1 Тесла – магнитная индукция такого однородного магнитного поля, кот действует с силой 1Н на каждый метр длины проводника с током 1А и расположенное ┴-о магнитному полю: 1Тл=1Н/(1А*1м). Из опытов вытекает, что для магнитных полей справедлив принцип суперпозиции:
. Сила Ампера нецентральная, т. е. зависит от ориентации проводника с током в магнитном поле. Из з-на Ампера обычно определяют магнитную индукцию (в-р) B. Пусть проводник прямолинейный и ┴-ый однородному магнитному полю (в-р) B: F=IlB, B=F/Il. Магнитная индукция (вектор) B – силовая, в-ная хар-ка магнитного поля, числ равная силе, действ- со стороны однородного магнитного поля на единицу длины проводника, по которому течет ток =1А и расположение проводника ┴-о напр магнитного поля. Ед изм В в системе СИ явл Тесла (Тл). 1 Тесла – магнитная индукция такого однородного магнитного поля, кот действует с силой 1Н на каждый метр длины проводника с током 1А и расположенное ┴-о магнитному полю: 1Тл=1Н/(1А*1м). Из опытов вытекает, что для магнитных полей справедлив принцип суперпозиции:  . Поле (в-р) B, порожденное несколькими движущими зарядами или токами, равно в-рной сумме полей (в-р)Bi, порожденных каждым зарядом или током в отдельности. Магнитное поле, как и эл-кое, изображается магнитными силовыми линиями – линиями (в-р) B. Линии магнитной индукции (в-р) B – это линии, касат к кот в каждой точке совпадают с напр в-ра B. Линии (в-р) B всегда замкнуты, что указывает на вихревой характер магнитного поля, на отсутствие магнитных зарядов, на кот могли бы начинаться и заканчиваться силовые линии. По густоте силовых линий судят о величине магнитного поля; там где силовые линии редкие – магнитное поле слабое.
. Поле (в-р) B, порожденное несколькими движущими зарядами или токами, равно в-рной сумме полей (в-р)Bi, порожденных каждым зарядом или током в отдельности. Магнитное поле, как и эл-кое, изображается магнитными силовыми линиями – линиями (в-р) B. Линии магнитной индукции (в-р) B – это линии, касат к кот в каждой точке совпадают с напр в-ра B. Линии (в-р) B всегда замкнуты, что указывает на вихревой характер магнитного поля, на отсутствие магнитных зарядов, на кот могли бы начинаться и заканчиваться силовые линии. По густоте силовых линий судят о величине магнитного поля; там где силовые линии редкие – магнитное поле слабое.
Линии индукции прямолинейного проводника с током представляют собой концентрические окружности, центры которых лежат на оси тока.
При поступательном движении правого винта направление вращения рукоятки винта указывает направление силовых линий.

 ρ
ρ 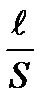 S,
S, 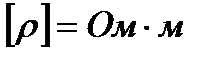

 (1+αtoC), I=
(1+αtoC), I=  , I=
, I=  ∙
∙  ∙S │:S,
∙S │:S,  =
=  ∙
∙ 
 - это закон Ома в диф.форме; если присутствуют сторонние силы:
- это закон Ома в диф.форме; если присутствуют сторонние силы: 
 Rt.
Rt.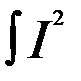 (t)Rdt
(t)Rdt
 =
=  = јE
= јE – закон Джоуля-Ленца в диф.форме
– закон Джоуля-Ленца в диф.форме ,т.к E=ј/σ, ω= ρ
,т.к E=ј/σ, ω= ρ 

 =0
=0 ток I входящий в узел счит «+»,вых «-».
ток I входящий в узел счит «+»,вых «-». =
=  При этом выбирают определённое направление обхода контура, если направление тока совпадает с направлением обхода контура то его считают положительным. ЭДС считают + если при выбранном направлении ток проходит от – к +. При этом число независимых уравнений получается меньше чем общее число контуров.
При этом выбирают определённое направление обхода контура, если направление тока совпадает с направлением обхода контура то его считают положительным. ЭДС считают + если при выбранном направлении ток проходит от – к +. При этом число независимых уравнений получается меньше чем общее число контуров. 1R1: I1r1+IR=
1R1: I1r1+IR= 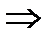 3. (1) (3) (4) позволяют найти токи I1 I2 I
3. (1) (3) (4) позволяют найти токи I1 I2 I Получим дифференциальную форму закона Ома из электронной связи:
Получим дифференциальную форму закона Ома из электронной связи: j=en<v>, I=q/t=enV/t=enSl/t=enSv, I/S=env, j=en<v>
j=en<v>, I=q/t=enV/t=enSl/t=enSv, I/S=env, j=en<v> . Ср время свободного пробега <τ> равно отношению ср длины св проб <l> к ср скор хаотического движения электронов <u>: <τ> =<l>/<u>. <v>=eE<l>/2m<u>. В этом случае мы пренебрегаем скоростью упорядоченного движения электронов в сравнении со скоростью хаотического, теплового движения электронов: <u> >> <v>: Т обр пол: j=e·n·e·E<l>/2m<u>=δE; δ=e2n<l>/2m<u> - электропроводность (j= δE). Если бы «е» не сталкивались с узлами решетки, то ср длина своб пробега l=∞ и электропроводность δ=∞ и не было бы эл-кого сопротивления. Тогда электрическое сопротивление мет в классической электронной теории вызвано столкновением свободных электронов с ионами решетки. По классической теории удельное сопротивление ρ=1/δ пропорционально средней скорости теплового движения <u>: <u>=√(8kT/2m)~√T. из опыта вытекает, что ρ=ρо(1+αT)
. Ср время свободного пробега <τ> равно отношению ср длины св проб <l> к ср скор хаотического движения электронов <u>: <τ> =<l>/<u>. <v>=eE<l>/2m<u>. В этом случае мы пренебрегаем скоростью упорядоченного движения электронов в сравнении со скоростью хаотического, теплового движения электронов: <u> >> <v>: Т обр пол: j=e·n·e·E<l>/2m<u>=δE; δ=e2n<l>/2m<u> - электропроводность (j= δE). Если бы «е» не сталкивались с узлами решетки, то ср длина своб пробега l=∞ и электропроводность δ=∞ и не было бы эл-кого сопротивления. Тогда электрическое сопротивление мет в классической электронной теории вызвано столкновением свободных электронов с ионами решетки. По классической теории удельное сопротивление ρ=1/δ пропорционально средней скорости теплового движения <u>: <u>=√(8kT/2m)~√T. из опыта вытекает, что ρ=ρо(1+αT)

 Оп путем было устан, что движущиеся эл-кие заряды, т. е. токи создают магнитные поля. Магнитное поле проявляется под действием сил магнитного взаимодействия. Магнитное поле в отличие от эл-кого действует только на движ заряды, на покоящиеся заряды не действует. (монополь – магнитный заряд) Сп-сть магнитного поля вызывать мех силу в каждой точке поля, действ на элемент тока Id(в-р)l хар-тся магнитной индукцией (вектор) B. Эл-т тока Id(в-р)l есть произв силы тока I на беск малый отрезок проводника d(в-р)l, направл по току. dI(в-р)l играет роль пробного заряда в электростатике. Ампер эксп-но установил, что сила d(в-р)F действ на элемент тока Id(в-р)l с индукцией (в-р) B равна:
Оп путем было устан, что движущиеся эл-кие заряды, т. е. токи создают магнитные поля. Магнитное поле проявляется под действием сил магнитного взаимодействия. Магнитное поле в отличие от эл-кого действует только на движ заряды, на покоящиеся заряды не действует. (монополь – магнитный заряд) Сп-сть магнитного поля вызывать мех силу в каждой точке поля, действ на элемент тока Id(в-р)l хар-тся магнитной индукцией (вектор) B. Эл-т тока Id(в-р)l есть произв силы тока I на беск малый отрезок проводника d(в-р)l, направл по току. dI(в-р)l играет роль пробного заряда в электростатике. Ампер эксп-но установил, что сила d(в-р)F действ на элемент тока Id(в-р)l с индукцией (в-р) B равна:  – закон Ампера (сила Ампера). Если проводник прямолинейный и магнитное поле однородное (одинаковое в каждой точке), интегрируя последнее выражение, получаем:
– закон Ампера (сила Ампера). Если проводник прямолинейный и магнитное поле однородное (одинаковое в каждой точке), интегрируя последнее выражение, получаем:  . Направление силы Ампера (в-р)F опр по правилу в-рного произведения. Сила (в-р)F ┴-а пл-сти, в кот лежат в-ры l и B и напр силы (в-р)F опред правилом правого винта: «если рукоятка правого винта вращается от первого вектора l ко второму ве-ру B на кратчайший угол, то поступательное движ винта указ направление силы (в-р)F». Модуль силы Ампера:
. Направление силы Ампера (в-р)F опр по правилу в-рного произведения. Сила (в-р)F ┴-а пл-сти, в кот лежат в-ры l и B и напр силы (в-р)F опред правилом правого винта: «если рукоятка правого винта вращается от первого вектора l ко второму ве-ру B на кратчайший угол, то поступательное движ винта указ направление силы (в-р)F». Модуль силы Ампера:  . Сила Ампера нецентральная, т. е. зависит от ориентации проводника с током в магнитном поле. Из з-на Ампера обычно определяют магнитную индукцию (в-р) B. Пусть проводник прямолинейный и ┴-ый однородному магнитному полю (в-р) B: F=IlB, B=F/Il. Магнитная индукция (вектор) B – силовая, в-ная хар-ка магнитного поля, числ равная силе, действ- со стороны однородного магнитного поля на единицу длины проводника, по которому течет ток =1А и расположение проводника ┴-о напр магнитного поля. Ед изм В в системе СИ явл Тесла (Тл). 1 Тесла – магнитная индукция такого однородного магнитного поля, кот действует с силой 1Н на каждый метр длины проводника с током 1А и расположенное ┴-о магнитному полю: 1Тл=1Н/(1А*1м). Из опытов вытекает, что для магнитных полей справедлив принцип суперпозиции:
. Сила Ампера нецентральная, т. е. зависит от ориентации проводника с током в магнитном поле. Из з-на Ампера обычно определяют магнитную индукцию (в-р) B. Пусть проводник прямолинейный и ┴-ый однородному магнитному полю (в-р) B: F=IlB, B=F/Il. Магнитная индукция (вектор) B – силовая, в-ная хар-ка магнитного поля, числ равная силе, действ- со стороны однородного магнитного поля на единицу длины проводника, по которому течет ток =1А и расположение проводника ┴-о напр магнитного поля. Ед изм В в системе СИ явл Тесла (Тл). 1 Тесла – магнитная индукция такого однородного магнитного поля, кот действует с силой 1Н на каждый метр длины проводника с током 1А и расположенное ┴-о магнитному полю: 1Тл=1Н/(1А*1м). Из опытов вытекает, что для магнитных полей справедлив принцип суперпозиции:  . Поле (в-р) B, порожденное несколькими движущими зарядами или токами, равно в-рной сумме полей (в-р)Bi, порожденных каждым зарядом или током в отдельности. Магнитное поле, как и эл-кое, изображается магнитными силовыми линиями – линиями (в-р) B. Линии магнитной индукции (в-р) B – это линии, касат к кот в каждой точке совпадают с напр в-ра B. Линии (в-р) B всегда замкнуты, что указывает на вихревой характер магнитного поля, на отсутствие магнитных зарядов, на кот могли бы начинаться и заканчиваться силовые линии. По густоте силовых линий судят о величине магнитного поля; там где силовые линии редкие – магнитное поле слабое.
. Поле (в-р) B, порожденное несколькими движущими зарядами или токами, равно в-рной сумме полей (в-р)Bi, порожденных каждым зарядом или током в отдельности. Магнитное поле, как и эл-кое, изображается магнитными силовыми линиями – линиями (в-р) B. Линии магнитной индукции (в-р) B – это линии, касат к кот в каждой точке совпадают с напр в-ра B. Линии (в-р) B всегда замкнуты, что указывает на вихревой характер магнитного поля, на отсутствие магнитных зарядов, на кот могли бы начинаться и заканчиваться силовые линии. По густоте силовых линий судят о величине магнитного поля; там где силовые линии редкие – магнитное поле слабое.


