 Пусть пробный зар. q* передвигается в Эл.п.. неподвижный зар. q на расстоянии dr и среда характеризующаяся диэлектрической проницаемостью
Пусть пробный зар. q* передвигается в Эл.п.. неподвижный зар. q на расстоянии dr и среда характеризующаяся диэлектрической проницаемостью  , тогда на зар. q* со стороны поля с напряженностью Е действует переменная сила
, тогда на зар. q* со стороны поля с напряженностью Е действует переменная сила  . элементарная работа dA этой силы = скалярному произведению:
. элементарная работа dA этой силы = скалярному произведению:  , напряж поля:
, напряж поля:  ,
,  . Пусть зар. перемещается из точки 1 в точку 2, тогда работа поля очевидно равна:
. Пусть зар. перемещается из точки 1 в точку 2, тогда работа поля очевидно равна:  . При любом выборе точек 1 и 2 работа не зависит от путей, точнее от формы траектории, а зависит от начального и конечного положения зар. q*.силовое поле такого рода называется потенциальным. Эл.п. неподвижного зар. потенциально(безвихривое). Электростатические силы консервативны. Если q* перемещается по замкнутому контуру, то
. При любом выборе точек 1 и 2 работа не зависит от путей, точнее от формы траектории, а зависит от начального и конечного положения зар. q*.силовое поле такого рода называется потенциальным. Эл.п. неподвижного зар. потенциально(безвихривое). Электростатические силы консервативны. Если q* перемещается по замкнутому контуру, то  , тогда
, тогда  . Поле потенциально, если работа сил поля по замкнутой траектории =0.
. Поле потенциально, если работа сил поля по замкнутой траектории =0.


 . Работа сил Эл.п. dA совершается за счет убыли его потенциальной энергии dW т.е.:
. Работа сил Эл.п. dA совершается за счет убыли его потенциальной энергии dW т.е.:
dA=-dW, тгда имеем  , проинтегрируем последнее выражение:
, проинтегрируем последнее выражение:  , Const интегрирования =0, т.к. при интегрировании r→
, Const интегрирования =0, т.к. при интегрировании r→  считается, что W=0,
считается, что W=0,  . Рассмотрим точку q.
. Рассмотрим точку q.
 Потенциал поля точки q на расстоянии r от зар. будет считаться равным:
Потенциал поля точки q на расстоянии r от зар. будет считаться равным:

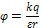
С учетом такого обозначения имеем: 
 . Потенциал
. Потенциал  есть скалярная энергетическая характеристика Эл.п., численно = потенциальной энергии единичного «+» зар. в данной точке поля:
есть скалярная энергетическая характеристика Эл.п., численно = потенциальной энергии единичного «+» зар. в данной точке поля:  =W при ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
=W при ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  =+1. Потенциал поля численно = отношению потенциальной энергии зар. данной точки поля к зар.(здесь знак зар. учитывается). Работу сил Эл.п. выразить через разность потенциалов:
=+1. Потенциал поля численно = отношению потенциальной энергии зар. данной точки поля к зар.(здесь знак зар. учитывается). Работу сил Эл.п. выразить через разность потенциалов:  , где
, где 
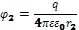
Работа сил Эл.п. при перемещении зар. численно = произведению величине этого зар. на разность потенциалов в начальной и конечной точке поля. Пусть точка 2 лежит в бесконечности, тогда можем написать:

 . Потенциал Эл.п.
. Потенциал Эл.п.  численно = работе сил поля при перемещении ед. «+» зар. из данной точки поля в
численно = работе сил поля при перемещении ед. «+» зар. из данной точки поля в  к зар. Другая характеристика:
к зар. Другая характеристика:
Разность потенциалов(или напряжение).
 , тогда
, тогда  *U U=
*U U=  - потенциал между точками 1и 2 измеряется работой совершенной силами поля при перемещении единичного «+» зар. из точки 1 в 2 по любому пути.
- потенциал между точками 1и 2 измеряется работой совершенной силами поля при перемещении единичного «+» зар. из точки 1 в 2 по любому пути.  . Для потенциала справедлив принцип суперпозиции: потенциал поля
. Для потенциала справедлив принцип суперпозиции: потенциал поля  системы точечных зар. = алгебраической сумме потенциалов создаваемых отдельными зар.
системы точечных зар. = алгебраической сумме потенциалов создаваемых отдельными зар. 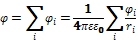
 Эквипотенциальная поверхность - пов. одинакового, разного потенциала, на которой
Эквипотенциальная поверхность - пов. одинакового, разного потенциала, на которой  , линии напряженности Е ортогональны (в частности перпендикулярны) к эквипотенциальной пов.
, линии напряженности Е ортогональны (в частности перпендикулярны) к эквипотенциальной пов.

 Пусть пробный зар. q* передвигается в Эл.п.. неподвижный зар. q на расстоянии dr и среда характеризующаяся диэлектрической проницаемостью
Пусть пробный зар. q* передвигается в Эл.п.. неподвижный зар. q на расстоянии dr и среда характеризующаяся диэлектрической проницаемостью  , тогда на зар. q* со стороны поля с напряженностью Е действует переменная сила
, тогда на зар. q* со стороны поля с напряженностью Е действует переменная сила  . элементарная работа dA этой силы = скалярному произведению:
. элементарная работа dA этой силы = скалярному произведению:  , напряж поля:
, напряж поля:  ,
,  . Пусть зар. перемещается из точки 1 в точку 2, тогда работа поля очевидно равна:
. Пусть зар. перемещается из точки 1 в точку 2, тогда работа поля очевидно равна:  . При любом выборе точек 1 и 2 работа не зависит от путей, точнее от формы траектории, а зависит от начального и конечного положения зар. q*.силовое поле такого рода называется потенциальным. Эл.п. неподвижного зар. потенциально(безвихривое). Электростатические силы консервативны. Если q* перемещается по замкнутому контуру, то
. При любом выборе точек 1 и 2 работа не зависит от путей, точнее от формы траектории, а зависит от начального и конечного положения зар. q*.силовое поле такого рода называется потенциальным. Эл.п. неподвижного зар. потенциально(безвихривое). Электростатические силы консервативны. Если q* перемещается по замкнутому контуру, то  , тогда
, тогда  . Поле потенциально, если работа сил поля по замкнутой траектории =0.
. Поле потенциально, если работа сил поля по замкнутой траектории =0.

 . Работа сил Эл.п. dA совершается за счет убыли его потенциальной энергии dW т.е.:
. Работа сил Эл.п. dA совершается за счет убыли его потенциальной энергии dW т.е.: , проинтегрируем последнее выражение:
, проинтегрируем последнее выражение:  , Const интегрирования =0, т.к. при интегрировании r→
, Const интегрирования =0, т.к. при интегрировании r→  считается, что W=0,
считается, что W=0,  . Рассмотрим точку q.
. Рассмотрим точку q. Потенциал поля точки q на расстоянии r от зар. будет считаться равным:
Потенциал поля точки q на расстоянии r от зар. будет считаться равным:
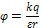

 . Потенциал
. Потенциал  есть скалярная энергетическая характеристика Эл.п., численно = потенциальной энергии единичного «+» зар. в данной точке поля:
есть скалярная энергетическая характеристика Эл.п., численно = потенциальной энергии единичного «+» зар. в данной точке поля:  =+1. Потенциал поля численно = отношению потенциальной энергии зар. данной точки поля к зар.(здесь знак зар. учитывается). Работу сил Эл.п. выразить через разность потенциалов:
=+1. Потенциал поля численно = отношению потенциальной энергии зар. данной точки поля к зар.(здесь знак зар. учитывается). Работу сил Эл.п. выразить через разность потенциалов:  , где
, где 
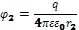

 . Потенциал Эл.п.
. Потенциал Эл.п.  численно = работе сил поля при перемещении ед. «+» зар. из данной точки поля в
численно = работе сил поля при перемещении ед. «+» зар. из данной точки поля в  , тогда
, тогда  *U U=
*U U=  - потенциал между точками 1и 2 измеряется работой совершенной силами поля при перемещении единичного «+» зар. из точки 1 в 2 по любому пути.
- потенциал между точками 1и 2 измеряется работой совершенной силами поля при перемещении единичного «+» зар. из точки 1 в 2 по любому пути.  . Для потенциала справедлив принцип суперпозиции: потенциал поля
. Для потенциала справедлив принцип суперпозиции: потенциал поля 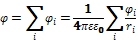
 Эквипотенциальная поверхность - пов. одинакового, разного потенциала, на которой
Эквипотенциальная поверхность - пов. одинакового, разного потенциала, на которой  , линии напряженности Е ортогональны (в частности перпендикулярны) к эквипотенциальной пов.
, линии напряженности Е ортогональны (в частности перпендикулярны) к эквипотенциальной пов.


