Принцип метода измерения
Интерференционная картина представляет собой совокупность чередующихся светлых и темных (красных и черных) полос (рис.2).
Рис. 2
Под шириной интерференционной полосы будем понимать общую ширину темной и светлой полос (совокупную ширину интерференционного максимума и минимума). Расчет ширины интерференционных полос, получающихся на экране, поясняет рис. 3.
Рис. 3
Ширина интерференционной полосы зависит от расстояния d между источниками света S 1 и S 2, длины световой волны l и от расстояния от источников до экрана L. Оптическая разность хода лучей от источников S 1 и S 2 равна Δ = S 2 – S 1. (3) Сумма расстояний от источников света до выбранной точки экрана с координатой X (при малых значениях X) приближенно равна S 2 + S 1 Квадрат расстояний от источников света S 1 и S 2 до выбранной точки экрана (рис. 3) может быть определен из уравнений S S Вычитая из (3) равенство (4) и раскрывая квадраты, получаем S Учитывая равенства (3) и (4), уравнение (7) представим в виде 2 L Δ = 2 xd. (8) Уравнения (9) и (10) являются условиями интерференционных максимумов и минимумов соответственно: Δ = ± m l (m = 0, 1, 2,...), (9) Δ = ±(m +1/2)l (m = 0, 1, 2,...). (10) Определим ширину интерференционной полосы как расстояние между соседними максимумами интенсивности освещенности экрана. Тогда из (8) и (9) следует Δ x = xm +1 – хm = l Такое же расстояние будет и между минимумами освещенности экрана. Отсюда длина световой волны, падающей на бипризму, равна l = Расстояние между мнимыми источниками d можно определить, зная преломляющий угол бипризмы q и ее показатель преломления n (см. рис. 1). d = 2 L 1 sinj Подставляя выражение (12) в (11), находим длину волны света, падающего на бипризму Френеля: l = 2 L 1(n – 1)q
|



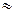 2 L. (4)
2 L. (4) = L 2 + (x + d /2)2, (5)
= L 2 + (x + d /2)2, (5)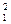 = L 2 + (x – d /2)2. (6)
= L 2 + (x – d /2)2. (6) .
. . (11)
. (11) . (13)
. (13)


