Краткая теория исследуемого явления. Если на струну натянутую между двумя точками, действует синусоидальная во времени сила, то струна колеблется
Если на струну натянутую между двумя точками, действует синусоидальная во времени сила, то струна колеблется. От того места, где на струну действует возбуждающая сила, влево и вправо бегут волны, многократно отражающиеся от закрепленных концов струны. В результате через каждую точку струны волны бегут в обоих направлениях. Поскольку частота колебаний этих волн задается синусоидальной силой, то в каждой точке имеет место сложение когерентных волн (т.е. волн с одинаковой частотой и неизменной разностью фаз в данном месте). Как известно, результатом такого сложения является интерференция. В случае, когда амплитуды встречных волн одинаковы (именно такой случай и рассматривается), возникает так называемая стоячая волна. Уравнения для встречных волн в произвольной точке х имеют вид:
где x – координата точки на струне, в которой наблюдают колебания; у1 – волна, бегущая в сторону возрастания координаты х; у2 – волна, бегущая в сторону убывания х;
Для упрощения будем рассматривать случай, когда у = у1+у2 = = Таким образом, в произвольной точке х возникает колебание с частотой вынуждающей силы Из уравнения (2) видно, что фаза колебаний ( В точках координаты (х), которые удовлетворяют условию
амплитуда колебаний максимальна и равна 2 А. Такие точки называются пучностями. А при условии
амплитуда колебаний равна 0, т.е. в этих точках колебаний нет. Такие точки называются узлами. Видно, что расстояние между соседними узлами равно Итак, при настройке струны в резонанс на ее длине l укладывается целое число n стоячих волн, т.е. n половин бегущей волны l = n ( Длина волны V = Согласно теории [ ] скорость распространения упругой волны в струне зависит от силы натяжения Р и линейной плотности V = Соотношение (7) можно представить в виде: V 2 = (P / При заданной частоте Длина волны
|


 , (1)
, (1) – длина волны;
– длина волны;  – сдвиг фаз между волнами, бегущими в противоположных направлениях.
– сдвиг фаз между волнами, бегущими в противоположных направлениях. +
+ 
 (2)
(2) (Т – период колебаний) с амплитудой 2А
(Т – период колебаний) с амплитудой 2А  , не зависящей от времени, но являющейся функцией координаты (х).
, не зависящей от времени, но являющейся функцией координаты (х). ) в точке х не зависит от координаты, как это имеет место для у 1 и у 2 по отдельности. Именно поэтому волну и называют стоячей.
) в точке х не зависит от координаты, как это имеет место для у 1 и у 2 по отдельности. Именно поэтому волну и называют стоячей.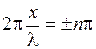 (n = 0,1,2…) (3)
(n = 0,1,2…) (3) (n = 0,1,2…) (4)
(n = 0,1,2…) (4) /2. Точки закрепления струны (концы) являются узлами, поэтому собственные установившиеся колебания струны возможны лишь при условии, что на длине струны укладывается целое число n полуволн. Если n = 1, то колебание называется основным, при n = 2 получается второй тип возможных собственных колебаний и т.д. При постоянном натяжении данной струны основному колебанию соответствует наименьшая частота (первая гармоника), второй тип колебания (вторая гармоника) получается при удвоенной частоте колебаний той же струны и т.д. Если частота вынуждающей силы совпадает с частотой одного из возможных колебаний, то наблюдается максимальное вынужденное колебание струны; это явление называется резонансом.
/2. Точки закрепления струны (концы) являются узлами, поэтому собственные установившиеся колебания струны возможны лишь при условии, что на длине струны укладывается целое число n полуволн. Если n = 1, то колебание называется основным, при n = 2 получается второй тип возможных собственных колебаний и т.д. При постоянном натяжении данной струны основному колебанию соответствует наименьшая частота (первая гармоника), второй тип колебания (вторая гармоника) получается при удвоенной частоте колебаний той же струны и т.д. Если частота вынуждающей силы совпадает с частотой одного из возможных колебаний, то наблюдается максимальное вынужденное колебание струны; это явление называется резонансом. ) и скорость волны V связаны соотношением:
) и скорость волны V связаны соотношением: (6)
(6) (массы одного метра длины струны) следующим образом:
(массы одного метра длины струны) следующим образом: (7)
(7) , скорость V можно определить исходя из соотношения (6).
, скорость V можно определить исходя из соотношения (6).


