Основные теоретические положения. Наряду с механическими колебаниями и колебательными системами существуют электрические, точнее электромагнитные
Наряду с механическими колебаниями и колебательными системами существуют электрические, точнее электромагнитные, колебания и колебательные системы. Такие колебательные системы являются непременной частью многих радиоприемных и передающих устройств.
Рис. 1 Простейшей электрической колебательной системой является так называемый последовательный колебательный контур, состоящий из последовательно подключенного резистора R, катушки индуктивности L и конденсатора С (рис.1). Если такой контур присоединить к источнику переменной ЭДС ( Согласно второму правилу Кирхгофа, действующая в контуре ЭДС равна сумме падений напряжений на его элементах:
где Падения напряжения соответственно равны
где q – заряд на обкладках конденсатора, Подставив в (1) выражения для
Продифференцируем это выражение по времени
Подставив
Частное решение этого уравнения будем искать в виде периодической функции от времени:
где I 0 – амплитуда тока, а φ – разность фаз между током и ЭДС. Составляя первую и вторую производные от тока I по времени, получим:
Из полученных соотношений видно, что напряжения на конденсаторе и катушке индуктивности сдвинуты по фазе на 1800, т.е. противофазны. Подставляя значения
Представляя
Так как это равенство должно выполняться для любого момента времени, то множители при
Из первого уравнения (6) имеем:
Возводя равенства (6) в квадрат и складывая их, найдем:
Таким образом, амплитуда тока в контуре равна
Равенства (5), (7) и (8) дают искомое решение: в цепи течет ток I того же периода, что и приложенная ЭДС; амплитуда этого тока I 0 определяется равенством (8). Токсдвинут по фазе относительно ЭДС на угол φ, определяемый равенством (7). Величина
а полное сопротивление достигает минимума и равно омическому сопротивлению Z = R; на этой частоте амплитуды падений напряжений на катушке индуктивности и на конденсаторе равны, а амплитуда силы тока достигает максимального значения:
Это явление носит название резонанса: амплитуда силы тока достигает максимума при некотором определенном значении частоты
Зависимость от частоты амплитуды тока I 0, а также напряжений U 0L и U 0C называют резонансными кривыми и имеют тем более острый максимум, чем меньше омическое сопротивлений R (рис.2 а,б):
а)
б) Рис. 2
Так как ток в цепи максимален, то на резонансной частоте падения напряжений на конденсаторе и катушке индуктивности достигают больших и одинаковых по амплитуде значений:
Величина По формуле (7) при резонансе разность фаз φ = 0. При Соотношения между переменным током I и напряжениями
Рис. 3 Отложим вдоль этого направления вектор тока длиной I 0. Посмотрим, как соотносятся вектора а) вектор UR = R I = b) вектор c) вектор Из рис.3 видно, что, как ранее было отмечено, вектора UL и UC направлены противоположно по отношению друг к другу. На резонансной частоте падение напряжения на катушке индуктивности и конденсаторе, согласно (9), равны. На резонансной частоте напряжения на катушке индуктивности и на конденсаторе компенсируют друг друга и ЭДС становится равной UR. Поэтому явление резонанса в последовательном контуре называется резонансом напряжений. Вне резонанса реактивное сопротивление контура уже не равно нулю, полное сопротивление Z возрастает, а амплитуда тока уменьшается по сравнению со значениями на резонансе. Качество колебательного контура характеризуется добротностью, которая обычно значительно больше единицы и равна отношению запасенной в контуре энергии за один период к теряемой контуром энергии (выделение тепла на омическом сопротивлении) за тот же период, и может быть определена как
Из выражений (11) видно, что на резонансе добротность показывает, во сколько раз на резонансе амплитуда напряжения на конденсаторе (или на катушке индуктивности) больше амплитуды ЭДС. Добротность характеризует остроту резонансных кривых и может быть непосредственно определена экспериментально. В случае малых значений затуханий (потерь) добротность определяется соотношением:
где
|



 ), то в таком контуре устанавливаются вынужденные гармонические колебания, совершающиеся с частотой ω источника.
), то в таком контуре устанавливаются вынужденные гармонические колебания, совершающиеся с частотой ω источника.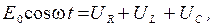 (1)
(1) – соответственно падения напряжения на резисторе, катушке индуктивности и конденсаторе.
– соответственно падения напряжения на резисторе, катушке индуктивности и конденсаторе. (2)
(2)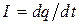
 – ток в контуре.
– ток в контуре. ,
,  и
и  из (2), получим
из (2), получим (3)
(3) .
. в это выражение, найдем дифференциальное уравнение вынужденных колебаний, которому должна удовлетворять сила тока в контуре: (1)
в это выражение, найдем дифференциальное уравнение вынужденных колебаний, которому должна удовлетворять сила тока в контуре: (1) (4)
(4) (5)
(5)
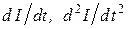 и I в уравнение (4) и разделив правую и левую части на ω, найдем:
и I в уравнение (4) и разделив правую и левую части на ω, найдем:
 и
и  через синусы и косинусы от ω t и φ, получим:
через синусы и косинусы от ω t и φ, получим:
 и
и 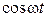 должны равняться нулю, откуда получаем два уравнения:
должны равняться нулю, откуда получаем два уравнения: (6)
(6) (7)
(7)
 (8)
(8) называется полным сопротивлением цепи, которое зависит как от значений R, L, C, так и от частоты тока ω, и состоит из активного (омического) R и полного реактивного сопротивлений
называется полным сопротивлением цепи, которое зависит как от значений R, L, C, так и от частоты тока ω, и состоит из активного (омического) R и полного реактивного сопротивлений  . Таким образом,
. Таким образом,  , где
, где  ,
, 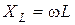 – индуктивное,
– индуктивное, 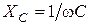 – емкостное реактивные сопротивления. При некоторой частоте ω = ω рез, называемой резонансной частотой, полное реактивное сопротивление обращается в нуль:
– емкостное реактивные сопротивления. При некоторой частоте ω = ω рез, называемой резонансной частотой, полное реактивное сопротивление обращается в нуль: (9)
(9)
 , которое совпадает с собственной частотой ω0 контура для незатухающих колебаний и значение которой в соответствии с формулой (9), равно:
, которое совпадает с собственной частотой ω0 контура для незатухающих колебаний и значение которой в соответствии с формулой (9), равно: . (10)
. (10)

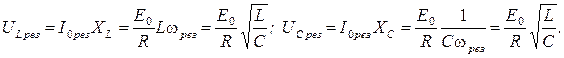 (11)
(11) называется волновым сопротивлением контура.
называется волновым сопротивлением контура. разность фаз
разность фаз  , т.е. ток опережает значение ЭДС; при
, т.е. ток опережает значение ЭДС; при  разность фаз
разность фаз  ; в этом случае ток отстает от ЭДС. На рис. 2а кривая 1 дает изменение силы тока с частотой при заданной ЭДС и постоянных L и C; кривая 2б дает зависимость сдвига фазы φ от частоты.
; в этом случае ток отстает от ЭДС. На рис. 2а кривая 1 дает изменение силы тока с частотой при заданной ЭДС и постоянных L и C; кривая 2б дает зависимость сдвига фазы φ от частоты.
 совпадает по направлению с вектором тока I. Отложим U 0R вдоль вектора тока.
совпадает по направлению с вектором тока I. Отложим U 0R вдоль вектора тока. ; т.е. напряжение UL опережает ток I на π/2. Отложим U 0L вертикально вверх.
; т.е. напряжение UL опережает ток I на π/2. Отложим U 0L вертикально вверх. ; т.е. напряжение UC отстает от тока I на π/2. Отложим U 0C вертикально вниз.
; т.е. напряжение UC отстает от тока I на π/2. Отложим U 0C вертикально вниз.
 (12)
(12) , следовательно,
, следовательно, (13)
(13) , где
, где  и
и  – частоты, на которых амплитуда тока в
– частоты, на которых амплитуда тока в  раз меньше резонансного значения. Добротность Q и логарифмический декремент колебаний λ контура связаны соотношением:
раз меньше резонансного значения. Добротность Q и логарифмический декремент колебаний λ контура связаны соотношением: