Анализ тренда динамического ряда
Проводим анализ возможного типа модели. Альтернативными являются: - линейная модель – модель равномерного увеличения размера номинальной среднемесячной заработной платы (Dц i» const); - экспоненциальная модель (Трц i» const). Для выбора оптимальной модели тренда определим степень вариации цепных показателей динамики – абсолютного цепного прироста Dц i и цепного темпа роста Трц i заработной платы. Для этого вычислим коэффициенты вариации данных показателей. Коэффициент вариации абсолютного цепного прироста
где Среднее квадратическое отклонение абсолютного цепного прироста находим по приближенной формуле (правило «трех сигм»):
где R∆ –размах абсолютного цепного прироста.
R∆ = ∆max - ∆min = 479 - (-28) = 507
Коэффициент вариации абсолютного цепного прироста рассчитываем по формуле:
Коэффициент вариации цепного темпа роста
где Среднее квадратическое отклонение цепного темпа роста также находим по правилу «трех сигм»:
где
Коэффициент вариации индекса сезонности рассчитываем по формуле:
Так как вариабельность цепного темпа роста значительно меньше изменчивости абсолютного цепного прироста (коэффициент вариации 3,4% и 35,4% соответственно), это свидетельствует о меньшей степени разброса значений абсолютного цепного прироста. Следовательно, на данном этапе анализа, в качестве оптимальной модели тренда выбираем экспоненциальную модель. .
|

 ,
,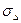 – среднее квадратическое отклонение абсолютного цепного прироста от его среднего значения;
– среднее квадратическое отклонение абсолютного цепного прироста от его среднего значения; 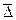 – значение среднего абсолютного прироста:
– значение среднего абсолютного прироста:
 ,
, - среднее квадратическое отклонение цепного темпа роста от его среднего значения;
- среднее квадратическое отклонение цепного темпа роста от его среднего значения; 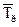 – среднее значение темпа роста.
– среднее значение темпа роста.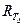 /6,
/6,



