Основные показатели динамики экономических явлений
Для анализа динамики социально-экономических явлений широко применяются следующие основные показатели динамики: - абсолютные приросты; - темпы роста; - темпы прироста. Каждый из указанных показателей рассчитывается в трех формах: - цепной; - базисный; - средний. В основе расчета показателей динамики лежит сравнение уровней ряда. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. В качестве базы сравнения выбирается обычно начальный уровень динамического ряда, Если каждый последующий уровень ряда сравнивается с предыдущим, то есть сравнение осуществляется при переменной базе, то вычисленные таким образом показатели называются цепными. Абсолютный прирост Dравен разности двух сравниваемых уровней – текущего и предыдущего, либо текущего и принятого за базу сравнения. Темп роста Трравен отношению двух сравниваемых уровней ряда (текущего и предыдущего, либо текущего и принятого за базу сравнения), выраженное в процентах или в коэффициентах. Определенный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Темп прироста Тпрхарактеризует абсолютный прирост изучаемого явления в относительных величинах. Ниже приведены выражения для вычисления базисных и цепных абсолютных приростов, темпов роста, темпов прироста. При этом используются следующие обозначения: хi – показатель для текущего (i -го) интервала времени; хi- 1 – показатель для предшествующего (i -1-го) интервала времени; х б – показатель для базового интервала времени. - базисный абсолютный прирост Dб i = хi – x б; - цепной абсолютный прирост Dц i = хi – xi -1; - базисный темп роста Трб i = 100 (хi / x б); - цепной темп роста Трц i = 100 (хi / xi -1); - базисный темп прироста Тпрб i = Трб i – 100; - цепной темп прироста Тпрц i = Трц i – 100. Для получения обобщающей характеристики развития изучаемого явления используют средние показатели динамики: средний уровень ряда, средний абсолютный прирост, средний темп роста и средний темп прироста. Расчет средних показателей динамики проводится по формулам: - средний уровень ряда - средний абсолютный прирост - средний темп роста - средний темп прироста Определение вида модели тренда осуществляется на основе анализа показателей динамики. Альтернативными являются: - линейная модель (для нее характерно примерное постоянство абсолютных цепных приростов Dц i»const); - экспоненциальная модель (для этой модели характерна устойчивость цепных темпов роста Трц i» const). В случае линейной модели тренда, для получения прогноза исследуемого показателя на период t (t –период упреждения ), необходимо воспользоваться следующей формулой:
где t – срок прогноза; i – номер последнего уровня ряда динамики; Если принимается экспоненциальная модель тренда, то прогноз исследуемого показателя рассчитывается по формуле:
где t – срок прогноза; i – номер последнего уровня ряда динамики; Методы среднего абсолютного прироста и среднего темпа роста являются простейшими, приближенными способами прогнозирования, они как правило предшествуют более глубокому качественному и количественному анализу временного ряда. Ниже приводится пример выполнения контрольной работы.
|

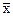 =
=  ;
;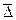 =
=  ;
; »
»  ;
; =
=  ,
, 
 ,
, – значение среднего темпа роста, рассчитанное для ряда динамики.
– значение среднего темпа роста, рассчитанное для ряда динамики.


