КОНТРОЛЬНАЯ РАБОТА №6
5. Поперечная волна распространяется вдоль упругого шнура с скоростью v = 10 м/с. Амплитуда колебаний точек шнура A = 5 см, период колебаний T = 1 с. Записать уравнение волны и определить: 1) длину волны, 2) фазу колебаний, смещение, скорость и ускорение точки, отстоящей на 9 м от источника колебаний в момент времени t 1 = 2,5 с. 6. Емкость конденсатора колебательного контура С = 39,5 мкФ, индуктивность его катушки L = 100 мГн. Заряд конденсатора q = 3 мкКл. Пренебрегая сопротивлением контура, записать уравнение 1) изменения силы тока в контуре в зависимости от времени, 2) изменения напряжения на конденсаторе в зависимости от времени. 7. В вакууме распространяется плоская электромагнитная волна, амплитуда напряженности электрического поля которой E m = 160 В/м. Определить амплитуду напряженности магнитного поля волны. ВАРИАНТ 1. 1. Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (λ1 = 500 нм) заменить красным (λ2 = 650 нм)? 2. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения (λ = 147 пм). Определить расстояние d между атомными плоскостями кристалла, если дифракционный максимум второго порядка наблюдается, когда излучение падает под углом θ = 31° 30′ к поверхности кристалла. 3. Естественный свет проходит через поляризатор и анализатор, установленные так, что угол между их плоскостями равняется φ. Как поляризатор, так и анализатор поглощают и отражают 8 % падающего на них света. Оказалось, что интенсивность луча, который вышел из анализатора, составляет 9 % интенсивности естественного света, который падает на поляризатор. Определить угол j. 4. Свет с длиной волны λ = 600 нм нормально падает на зеркальную поверхность и производит на нее давление p = 4 мкПа. Определить число N фотонов, падающих за время t = 10 с на площадь S = 1 мм2 этой поверхности. 5. При фотоэффекте с платиновой поверхности электроны полностью задерживаются разностью потенциалов U = 0,8 В. Определить длину волны l примененного излучения и предельную длину волны l0, при которой еще возможен фотоэффект. 6. Зачерненный шарик остывает от температуры Т 1 = 300 К до Т 2 = 200 К. На сколько изменилась длина волны l, которая соответствует максимуму спектральной плотности энергетической светимости? 7. Какой была длина волны l рентгеновского излучения, если при комптоновском рассеянии этого излучения графитом под углом θ = 60° длина волны рассеянного излучения оказалась равной l¢ = 25,4 пм?
ВАРИАНТ 2. 1. В опыте Юнга отверстия освещались монохроматическим светом (λ = 600 нм). Расстояние между отверстиями d = 1 мм, расстояние от отверстий до экрана L = 3 м. Определить положение третьей светлой полосы. 2. На дифракционную решетку нормально падает пучок монохроматического света. Максимум третьего порядка наблюдается под углом φ = 36° 48' к нормали. Определить постоянную d решетки, выраженную в длинах волн падающего света. 3. Определить угол φ между плоскостями поляризатора и анализатора, если интенсивность естественного света, который проходит через поляризатор и анализатор, уменьшается в 4 раза. 4. Какую мощность P надо подводить к зачерненному металлическому шарику радиусом r = 2 см, чтобы поддерживать его температуру на D Т = 27К выше температуры окружающей среды? Температура окружающей среды Т = 293 К. Считать, что тепло теряется только вследствие излучения. 5. Определить длину волны l0 света, который соответствует красной границе фотоэффекта для лития, натрия, калия и цезия. 6. Определить длину волны λ фотона, масса которого равняется массе покоя: 1) электрона; 2) протона. 7. На поверхность, которая идеально отражает, в течение времени t = 3 мин нормально падает монохроматический свет, энергия которого W = 9 Дж. Площадь поверхности S = 5 см2. Определить давление света на поверхность.
ВАРИАНТ 3.
1. В опыте Юнга на пути одного из интерферирующих лучей размещалась тонкая стеклянная пластинка, вследствие чего центральная светлая полоса смещалась в положение, которое сначала было занято пятой светлой полосой (не считая центральной). Луч падает перпендикулярно к поверхности пластинки. Показатель преломления пластинки n = l,5. Длина волны λ = 600 нм. Какова толщина h пластинки? 2. На щель шириной а = 2 мкм падает нормально параллельный пучок монохроматического света (λ = 589 нм). Определить ширину А изображения щели на экране, удаленном от щели на расстояние l = 1 м. Шириной изображения считать расстояние между первыми дифракционными минимумами, размещенными по обе стороны от главного максимума освещенности. 3. Пучок естественного света, который идет в воде, отражается от грани алмаза, погруженного в воду. При каком угле падения i В отраженный свет целиком поляризован? 4. Поверхность тела нагрета до температуры Т = 1 000 К. Потом одна половина этой поверхности нагревается на D Т = 100 К, другая охлаждается на Δ Т = 100 К. Во сколько раз изменится энергетическая светимость R э поверхности тела? 5. Длина волны света, которая соответствует красной границе фотоэффекта, для некоторого металла l0 = 275 нм. Определить минимальную энергию e фотона, который вызовет фотоэффект. 6. Давление р монохроматического света (l = 600 нм) на черную поверхность, расположенную перпендикулярно падающим лучам, равно 0,1 мкПа. Определить количество N фотонов, которые падают за время t = 1 с на поверхность площадью S = 1 см2. 7. Рентгеновское излучение с длиной волны l = 20 пм испытывает комптоновское рассеяние под углом θ = 90°. Определить изменение Dl длины волны рентгеновского излучения при рассеянии, а также энергию и импульс электрона отдачи. ВАРИАНТ 4.
1. На тонкий клин в направлении нормали к его поверхности падает монохроматический свет (λ = 600 нм). Определить угол α между поверхностями клина, если расстояние b между соседними интерференционными минимумами в отраженном свете равно 4 мм. 2. Точечный источник света (λ = 0,5 мкм) расположен на расстоянии а = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определить расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля. 3. Угол Брюстера i В при падении света из воздуха на кристалл каменной соли равен 57°. Определить скорость света в этом кристалле. 4. Абсолютно черное тело имеет температуру Т 1 = 2 900 К. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на Dl = 9 мкм. До какой температуры Т 2 охладилось тело? 5. Длина волны света, которая соответствует красной границе фотоэффекта, для некоторого металла l0 = 275 нм. Определить работу выхода А электрона из металла, максимальную скорость v max электронов, которые вырываются из металла светом с длиной волны l = 180 нм, и максимальную кинетическую энергию W max электронов. 6. Монохроматическое излучение с длиной волны l = 500 нм падает нормально на плоскую зеркальную поверхность и давит на нее с силой F = 10 нН. Определить количество N 1 фотонов, которые каждую секунду падают на эту поверхность. 7. Определить энергию ε, массу m и импульс р фотона, если соответствующая ему длина волны λ1 = 1,6 пм.
ВАРИАНТ 5.
1. На мыльную пленку падает белый свет под углом i = 45° к ее поверхности. При какой наименьшей толщине h пленки отраженные лучи будут иметь желтый цвет (λ = 600 нм)? Показатель преломления мыльной воды n = 1,33. 2. Какой должна быть постоянная d дифракционной решетки, чтобы в первом порядке были разрешены линии спектра калия λ1 = 404,4 нм и λ2 = 404,7 нм? Ширина решетки а = 3 см. 3. Предельный угол i пр полного отражения пучка света на границе жидкости с воздухом равен 43°. Определить угол Брюстера i В для падения луча из воздуха на поверхность этой жидкости. 4. Во сколько раз надо увеличить термодинамическую температуру черного тела, чтобы его энергетическая светимость R е возросла в два раза? 5. Параллельный пучок монохроматического света (λ = 662 нм) нормально падает на зачерненную поверхность и производит на нее давление р = 0,3 мкПа. Определить концентрацию n фотонов в световом пучке. 6. Определить угол θ рассеяния фотона, испытавшего соударение со свободным электроном, если изменение длины волны при рассеянии Δλ = 3,63 пм. 7. Определить массу m фотона: а) видимого света (λ1 = 700 нм); б) рентгеновских лучей (λ1 = 25 пм); в) гамма-лучей (λ = 1,6 пм).
ВАРИАНТ 6.
1. Мыльная пленка расположена вертикально и образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном свете ртутной дуги (λ = 546,1 нм) оказалось, что расстояние между пятью полосами l = 2 см. Определить угол α клина. Свет падает перпендикулярно поверхности пленки. Показатель преломления мыльной воды n = 1,33. 2. Плоская световая волна (l = 0,7 мкм) падает нормально на диафрагму с круглым отверстием радиусом r = 1,4 мм. На пути лучей, прошедших через отверстие, помещен экран. Определить максимальное расстояние b max от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно. 3. Коэффициент поглощения некоторого вещества для монохроматического света определенной длины волны α = 0,1 см–1. Определить толщину слоя вещества, которая необходима для ослабления света в 2 раза. 4. Определить относительное увеличение D R е/ R е энергетической светимости черного тела при увеличении его температуры на 1%. 5. Определить частоту ν света, который вырывает из металла электроны, если они целиком задерживаются разностью потенциалов U = 3 В. Фотоэффект начинается при частоте света ν0= 6∙1014 Гц. Найти работу выхода А электрона из металла. 6. Фотон с длиной волны λ = 15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона λ′ = 16 пм. Определить угол θ рассеяния. 7. С какой скоростью v должен двигаться электрон, чтобы его кинетическая энергия равнялась энергии фотона с длиной волны l = 520 нм? ВАРИАНТ 7.
1. На пути световой волны, которая распространяется в воздухе, поставили стеклянную пластинку толщиной h = 1 мм. На сколько изменится оптическая длина пути, если волна падает на пластинку: 1) нормально; 2) под углом i = 30°? 2. Постоянная дифракционной решетки d = 2 мкм. Какую разность длин волн Δλ может разрешить эта решетка в области желтых лучей (λ = 600 нм) в спектре второго порядка? Ширина решетки a = 2,5 см. 3. Угол φ между плоскостями поляризатора и анализатора равен 45°. Во сколько раз уменьшится интенсивность света, который выходит из анализатора, если угол увеличить до 60°? 4. Температура Т верхних слоев звезды Сириус равна 10 кК. Определить поток энергии Фе, который излучается с поверхности площадью S = 1 км2 этой звезды. 5. Фотоны с энергией e = 4,9 эВ вырывают электроны из металла с работой выхода А = 4,5 эВ. Определить максимальный импульс p max, сообщенный поверхности металла при вылете каждого электрона. 6. С какой скоростью v должен двигаться электрон, чтобы его импульс равнялся импульсу фотона с длиной волны l = 520 нм? 7. Энергия рентгеновских фотонов ε = 0,6 МэВ. Определить энергию электрона отдачи, если длина волны рентгеновских лучей после комптоновского рассеяния изменилась на 20%.
ВАРИАНТ 8.
1. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны l = 600 нм, который падает по нормали к поверхности пластинки. Определить толщину h воздушного зазора между линзой и стеклянной пластинкой в том месте, где наблюдается четвертое темное кольцо в отраженном свете. 2. На дифракционную решетку падает нормально пучок света. Красная линия (λ = 700 нм) в спектре первого порядка видна под углом дифракции φ = 30°. Определить постоянную d дифракционной решетки. Какое количество штрихов N 0 нанесено на единицу длины этой решетки? 3. Во сколько раз ослабляется интенсивность естественного света, который проходит через два поляризатора, плоскости которых образуют угол φ = 30°? 4. В каких областях спектра лежат длины волн, которые соответствуют максимуму спектральной плотности энергетической светимости, если источником света служит: а) спираль электрической лампочки (Т = 3 000 К); б) поверхность Солнца (Т = 6 000 К); в) атомная бомба, в которой в момент взрыва развивается температура Т» 107 К? 5. Определить постоянную Планка h, если известно, что электроны, которые вырываются из металла светом с частотой v1 = 2,2·1015 Гц, полностью задерживаются разностью потенциалов U 1 = 6,6 В, а те, которые вырываются светом с частотой v2 = 4,6·1015 Гц, – разностью потенциалов U 2 = 16,5 В. 6. На плоскую идеально отражающую поверхность нормально падает монохроматический свет с длиной волны l = 0,55 мкм. Поток излучения Фе составляет 0,45 Вт. Определить силу давления, которую испытывает эта поверхность. 7. Какую энергию ε должен иметь фотон, чтобы его масса равнялась массе покоя электрона?
ВАРИАНТ 9.
1. Расстояние Dr1,2 между первым и вторым темными кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние D r 9,10 между девятым и десятым кольцами. 2. Свет от монохроматического источника (λ = 600 нм) падает нормально на диафрагму с диаметром отверстия d = 6 мм. За диафрагмой на расстоянии l = 3 м от нее помещен экран. Какое количество k зон Френеля укладывается в отверстии диафрагмы? Каким будет центр дифракционной картины на экране: темным или светлым? 3. Определить показатель преломления стекла, если при отражении от него света отраженный луч полностью поляризован в случае, когда угол преломления составляет 35°. 4. Поток энергии Ф, который излучается из окошка плавильной печи, равен 34 Вт. Определить температуру Т, если площадь отверстия S = 6 см2. 5. Определить максимальную скорость vmax фотоэлектронов, вылетающих из металла при облучении γ–фотонами с энергией ε = 1,53 МэВ. 6. При какой температуре Т кинетическая энергия молекулы двухатомного газа будет равняется энергии фотона с длиной волны λ = 589 нм? 7. Фотон с энергией 100 кэВ вследствие эффекта Комптона рассеялся при столкновении со свободным электроном на угол q = p/2. Определить энергию фотона после рассеяния.
ВАРИАНТ 10.
1. На поверхность стеклянного объектива (n 1 = 1,5) нанесена тонкая пленка, показатель преломления которой n 2 = 1,2 (пленка, которая „просветляет”). При какой наименьшей толщине d этой пленки произойдет максимальное ослабление отраженного света в средней части видимого спектра? 2. Определить наибольший порядок m спектра для желтой линии натрия (λ = 589 нм), если постоянная дифракционной решетки d = 2 мкм. 3. Определить, под каким углом к горизонту должно находиться Солнце, чтобы отраженные от поверхности воды (n = 1,33) лучи были полностью поляризованными. 4. Определить температуру Т, при которой энергетическая светимость R e абсолютно черного тела равняется 10 кВт/м2. 5. Определить задерживающее напряжение U для электронов, которые вырываются при облучении калия светом с длиной волны l = 330 нм. 6. На зеркальную поверхность площадью S = 6 см2 падает нормально поток излучения Φ = 0,8 Вт. Определить давление p и силу давления F света на эту поверхность. 7. Определить длину волны l фотона, импульс которого равняется импульсу электрона, движущемуся со скоростью v = 10 Мм/с. КОНТРОЛЬНАЯ РАБОТА №6 ВАРИАНТ 1
1. Заряженная частица, ускоренная разностью потенциалов U = 200 В, имеет длину волны де Бройля l = 2,02 пм. Определить массу m частицы, если ее заряд численно равен заряду электрона. 2. Определить в электрон-вольтах максимальную энергию Е фонона, который может возбуждаться в кристалле NaCl, если характеристическая температура Дебая T D = 320 К. Фотон какой длины волны λ обладал бы такой энергией? 3. Какую наименьшую энергию Е нужно затратить, чтобы оторвать один нейтрон от ядра азота 147 N? 4. Определить промежуток времени τ, в течение которого активность А изотопа стронция 90Sr уменьшится в k 1 = 10 раз? В k 2 = 100 раз? Период полураспада стронция Т 1/2 = 28 лет. 5. Какая энергия D Е выделяется при термоядерной реакции синтеза 21H + 31H → 42He + 10n? Ответ дать в джоулях и электрон-вольтах.
 а.е.м. а.е.м.
ВАРИАНТ 2
1. Определить длину волны де Бройля l для: а) электрона, движущегося со скоростью v = 106 м/с; б) атома водорода, движущегося со средней квадратичной скоростью при температуре Т = 300 К; в) шарика массой m = 1 г, движущегося со скоростью v = 1 см/с. 2. Что такое фонон, каковы его свойства? 3. Энергия связи Е св ядра кислорода 188 O равна 139,8 МэВ, ядра фтора 199 F - 147,8 МэВ. Определить, какую минимальную энергию Е нужно затратить, чтобы оторвать один протон от ядра фтора. 4. Определить массу m полония 210 84Ро, активность которого А = 3,7∙1010 Бк. Период полураспада полония Т 1/2 = 138 сут. 5. Написать недостающие обозначения в реакциях: а) в)
ВАРИАНТ 3
1. Определить дебройлевскую длину волны λ шарика массой m = 1 г, движущегося со скоростью v = 100 м/с. Можно ли обнаружить волновые свойства такого шарика, и почему 2. Объяснить физический смысл энергии Ферми. 3. Определить энергию связи Е св ядра изотопа лития 73Li. 4. Какая часть η начального числа ядер 90Sr распадется за одни сутки и за 15 лет? Какая часть ζ останется через 10 лет и через 100 лет? Период полураспада стронция Т 1/2 = 28 лет. 5. Определить наименьшую энергию g-кванта, достаточную для осуществления реакции разложения дейтона g-лучами
ВАРИАНТ 4
1. Определить квантовомеханическую неопределенность Δ v x х -компоненты скорости частицы массой m = 1 г и электрона, если положение каждого из них определено с одинаковой ошибкой ∆ х = 10–7м. 2. Пояснить физический смысл характеристической температуры Дебая. 3. Определить энергию связи Е св ядра атома гелия 42He. 4. Вследствие последовательных радиоактивных распадов ядро урана 5. При бомбардировке изотопа азота
ВАРИАНТ 5
1. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определить (в электрон-вольтах) неопределенность кинетической энергии этого электрона. 2. В германии с примесью бора энергия активации примесных атомов Δ Е п = 0,01 эВ. Определить: 1) тип проводимости примесного полупроводника; 2) тип примесной фотопроводимости; 3) красную границу фотопроводимости. 3. Определить энергию связи Е св ядра атома алюминия 4. Определить постоянную радиоактивного распада λ ядра 55Co, если за час распадается 4% начального числа ядер. Продукт распада стабильный. 5. Определить суточный расход ядерного горючего 235U в реакторе АЭС. Тепловая мощность станции равна Р = 10 МВт. Принять, что в одном акте деления выделяется энергия Q = 200 МэВ, а КПД станции равен η = 0,2 (20%).
ВАРИАНТ 6
1. Электрон находится в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной l. Определить, в каких точках интервала ( 2. В чем смысл понятия «дырка» как носителя тока в полупроводнике? Существуют ли дырки вне полупроводника? Совпадают ли зоны проводимости для электронов и дырок в полупроводниках? Чему равна наименьшая энергия emin образования пары электрон-дырка в собственном полупроводнике, проводимость которого возрастает в n = 2 раза при повышении температуры от T 1 = 300 K до T 2= 310 К? 3. Определить энергию связи Е св ядер: а) 4. За один год начальное количество радиоактивного препарата уменьшилось в 5 раз. Во сколько раз оно уменьшится за два года? 5. Определить энергию Е, которая высвободится при соединении одного протона и двух нейтронов в атомное ядро.
ВАРИАНТ 7
1. Электрон в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной l находится в нижнем возбужденном состоянии. Какова вероятность обнаружения электрона в интервале l /4, равноудаленном от стенок ямы? 2. Определить ширину D Е запрещенной зоны теллура, если его электропроводность возрастает в n = 5 раз при повышении температуры от T 1=300 K до T 2= 400 K. 3. Определить энергию связи Е св, приходящуюся на один нуклон в ядрах; a) 4. Определить количество D N атомов, которые распались в m = 1 мг радиоактивного натрия 2411Na за время t 1= 10 час. Период полураспада натрия Т 1/2= 15,3 час. 5. Определить энергию Q ядерной реакции: 4420Са +11Н→4119К+42He.
ВАРИАНТ 8
1. Частица в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной l находится в основном состоянии, которому соответствует энергия Е 1 = 8,12 МэВ. Ширина ямы l = 5∙10–15 м. Определить массу m частицы. 2. Кремниевый образец нагревают от 0 до 10 °С. Принимая ширину D Е запрещенной зоны кремния 1,1 эВ, определить, во сколько раз возрастет его удельная проводимость. 3. Энергия связи Е св ядра, состоящего из двух протонов и одного нейтрона, равна 7,72 МэВ. Определить массу m a нейтрального атома, имеющего это ядро. 4. Сколько атомов из N = 106 атомов полония распадается за время t = 1 сут? Период полураспада полония Т 1/2 = 138 сут. 5. Определить энергию Q, выделяющуюся при реакции
ВАРИАНТ 9
1. Рассматривая приближенно ядро и атом как одномерные прямоугольные бесконечно глубокие потенциальные ямы для электронов и нуклонов, вычислить расстояние между основным и первым возбужденным уровнями в атоме Δ Е а1,2 и ядре Δ Е я1,2, полагая, что для атома l а = 5∙10–10 м, а для ядра l я = 5∙10–15 м. 2. Удельная проводимость кремния имеет значение σ1 =19 См/м при температуре T 1= 600 Kи σ2 =4 095 См/м при T 2= 1 200 K. Определить ширину D Е запрещенной зоны для кремния. 3. Определить массу m a нейтрального атома, если ядро этого атома состоит из трех протонов и двух нейтронов и энергия связи Е св ядра равна 26,3 МэВ. 4. За время t =1 сут активность изотопа уменьшилась от А 1 = 118 ГБк до А 2 = 7,4 ГБк. Определить период полураспада T 1/2 этого нуклида. 5. Определить энергию Q, поглощающуюся при реакции
ВАРИАНТ 10
1. Электрон с энергией Е = 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U 0 = 10 эВ и шириной l = 0,1 нм. Определить для этого барьера коэффициент прозрачности D. 2. В кремнии с примесью мышьяка энергия активации примесных атомов Δ Е п = 0,05 эВ. Определить: 1) тип проводимости примесного полупроводника; 2) тип примесной фотопроводимости; 3) максимальную длину волны, при которой фотопроводимость еще возбуждается. 3. Определить энергию связи, приходящуюся на один нуклон Е св/ A в ядрах; a) 73 Li; б) 147 N; в) 2713 А1; г) 4020 Са; д) 6329 Cu; e) 11348 Cd; ж) 20080 Hg; з) 23892 U. Построить зависимость Е св/ A = ƒ(А), где А – массовое число. 4. Определить постоянную распада λ радона, если известно, что число атомов радона уменьшается за время t = 1 сут на 18,2%. 5. Определить энергию Q, выделяющуюся при реакции:
|

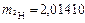 а.е.м.
а.е.м.  а.е.м.
а.е.м.  а.е.м.
а.е.м.
 ; б)
; б)  ;
; ; г)
; г)  .
. .
. превратилось в ядро свинца
превратилось в ядро свинца  . Пользуясь таблицей Менделеева, определить сколько актов α-распада и β-распада при этом произошло.
. Пользуясь таблицей Менделеева, определить сколько актов α-распада и β-распада при этом произошло. нейтронами получается изотоп углерода
нейтронами получается изотоп углерода 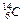 , который оказывается b - радиоактивным. Написать уравнения обеих реакций.
, который оказывается b - радиоактивным. Написать уравнения обеих реакций. .
. ) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова. Вычислить плотность вероятности для этих точек. Пояснить графически.
) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова. Вычислить плотность вероятности для этих точек. Пояснить графически. ; б)
; б)  . Какое из этих ядер более устойчиво?
. Какое из этих ядер более устойчиво?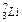 ; б)
; б) 
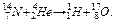
 .
.


