Заміна загального представлення функцій значеннями окремих типових ланок.
Відповідно до (5.4) W (p) = ( 6 Методика виконання завдання № 6 [1, 2]
ЗНАЙТИ КІЛЬКІСТЬ ДОРІЖОК КОДОВОГО ДАТЧИКА, ЩОБ ВІН ПРАЦЮВАВ ІЗ ЗАДАННОЮ ТОЧНІСТЮ В теперішній час найбільш перспективними для вимірювання переміщень є магнітні зубчасті, циклічні датчики з сінус-косінусними і лінійними індукційними перетворючами, фотоелектричні з дифракційними ґратками і датчики з вимірювальними дисками, кодовими масками. Для вимірювання лінійних переміщень використовують магнітний зубчастий датчик (рис. 6.1). Датчик складається із магнітної шкали 1 із зубцями кроку p 1 і магнітної головки, що виконана з двох П-подібних осердь 4 і 6, на кінці яких нанесені зубці кроку p 2, який відповідає умові p 2 = p 1 /K,(6.1) де K -ціле число. Зубці одного із осердь головки розташовані із зсувом відносно зубців другого осердя на половину кроку нарізки. На осердях намотана обмотка 5, що намагнічує і дві вихідні обмотки 2 і 7, що підключені через випрямлячі з ємнісними фільтрами 3 і 8 за диференційною схемою до навантаження 9. При відносному переміщенні шкали 1 і магнітної головки провідність в магнітних колах між осердями і шкалою змінюється з періодом, що відповідає кроку нарізки осердь.
Магнітний потік Ф 1, що утворюється первиною обмоткою, перерозподіляється відповідно магнітним провідностям gМ2 і gМ3 осердь 4 і 6. Магнітні потоки, що пересікають вторіні обмотки головки, відповідно дорівнюють
Ф 2 = Ф 1 g М2 /(gМ2 + gМ3 ) 6.2) і Ф 3 = Ф 1 gМ3 /(gМ2 + gМ3).(6.3)
У вторинних обмотках магнітної головки наводяться ЕРС, що пропорційні зміненню магнітних потоків Ф 2 і Ф 3 і зміщені відносно один одного. Після випрямляння і віднімання сигналів з урахуванням рівності сталих складових ЕРС на виходах 3 і 8 отримаємо
Е = Е 2(D L) - E 3(D L), (6.4)
де Е2 (D L), Е 3(D L) - зміні складові ЕРС на виходах випрямлячів 3 і 8, що залежать від переміщення D L магнітної шкали 1. Після розкладання у ряд Фур’є функцій Е 2(D L) і Е3( D L), що є парними і зсунутими відносно одна одної наp, на навантажені 9 отримаємо сигнал
L = 0,5(а О2 - а О3) + Тут j = 2p D L/p 2. Припускаючи, що амплітуди гармонік функцій Е 2(D L) і E3 (D L) дорівнюють одна одній, тобто аn = an 2 = an 3,..., a 1= a 12 = a 13, a0 = a0 2 = a0 3, при зміні n = 1... ¥, отримуємо
Графічна залежність результатного сигналу від величини переміщення наведена на рис. 6.1, б. Як видно із графіку, нульові значення вихідного сигналу зміщені один від одного на половину кроку p 2. Ціна ділення 0,02 мм.
Для підвищення точності виміру лінійних переміщень використовують лінійні фотоелектричні датчики з дифракційними ґратками (інтерферометри). Джерело монохроматичного випромінювання 1 (рис. 6.2) просвічує дві дифракційні ґратки у вигляді нерухомої 2 і рухомої 3 лінійок під час роботи датчика. Ґратки виконані із пластин скла, на які нанесені риски у вигляді смуг золота з кроком, величина якого становить від 1 до 10 мкм. Риски наносять на лінійку 2 перпендикулярно, а на лінійку 3 під деяким кутом до напрямку руху об’єкта виміру. При русі об’єкта разом з ним переміщується лінійка 3, фотоелементи 4 і 6 сприймають світловий потік у вигляді темних і світлих смуг (муарові смуги переміщуються вверх або вниз в залежності від напрямку руху відповідно праворуч або ліворуч лінійки 3). Фотоелемент 4 перетворює муарові смуги в електричні імпульси, які є джерелом інформації. Фотоелемент 6 призначено для визначення напрямку руху об’єкта. Ціна ділення 0,5 мкм. Для виміру кутових і лінійних переміщень з великою точністю часто використовують трансформатори, що обертаються (індуктосини), які уявляють собою електричну мікромашину змінного струму з двофазними обмотками на роторі і статорі. Трансформатори, що обертаються перетворюють кут оберту ротора в зміну амплітуди або фази синусоїдальної напруги.
Трансформатори, що обертаються, можуть працювати в режимах фазообертовому або синусно-косинусному. В режимі фазообертовому в первинні обмотки трансформатора, що обертається, подають два сигнали синусоїдальної форми, однакові за амплітудою, але зсунуті за фазою один відносно одного на p/2. При цьому у вторинній обмотці індукується ЕРС, фаза якої змінюється лінійно в залежності від кута оберту. У синусно-косинусному режимі на виході трансформатора, що обертається формуються синусоїдальні коливання, що зсунуті на p/2, амплітуда яких пропорційна куту оберту ротора. Трансформатори, що обертаються мають клас точності 0,02; 0,05 і 0,1. Індуктосини це багато полюсні трансформатори (без магнітних осердь), обмотки яких виконані фотохімічним методом. Статорна обмотка індуктосина виконується у вигляді лінійки 1 (рис. 6.3), по якій ковзає головка 2 (роторна обмотка). На лінійці і головці нанесені друкувальним способом обмотки 3, 4 і 5. Роторні обмотки 3 і 4 зсунуті одна відносно другої на 1/4 кроку. При живлені однієї обмотки синусоїдальною напругою з частотою порядку 10 кГц на другій обмотці індукується ЕРС, що зміщена на p/2. Між головкою і лінійкою виникає рухоме магнітне поле, яке індукує на статорній обмотці 5 лінійки ЕРС, фаза якої визначається відносним лінійним переміщенням лінійки і головки. Точність ± 2,5 мкм на довжині 250 мм і більше. Всі розглянуті датчики відносяться до циклічних. Циклічні датчики формують значення, що періодично повторюються. При цьому виміряний параметр перетворюється у часовий інтервал. Такі датчики звичайно складаються з двох пристроїв: точного і грубого відліку. Пристрої точного відліку багаторазово повторюють цикл виміру за один оберт, що вносить неоднозначність у вимірювання кута повороту вала двигуна. Для усунення неоднозначності і визначення абсолютного значення параметра використовують пристрій грубого відліку, який проводить підрахунок кількості повних циклів роботи датчика від нульової позначки. До нециклічних датчиків відноситься кодовий датчик. Кодовий датчик складається із кодової лінійки (диска), освітлювальної лампи, блока фотодіодів і комбінованого блока. Він призначається для перетворення лінійних (кутових) переміщень у двійковий код і передачі його в автоматичну систему керування (АСК). Датчик працює так: промінь світла від джерела попадає на кодову лінійку (диск) (рис. 6.4), проходить крізь прозорі ділянки, попадає в блок фотодіодів. Фотодіоди 1...6 формують сигнали 1 і 0. Кодовий диск виконується фотохімічним способом в двійковому рефлексному коді і складається із n доріжок. Величина n визначається необхідною точністю виміру параметра.
Так, при заданій похибці перетворення в 0,1 % кількість ділень шкали кодового диска дорівнює 1000. Останній складається із 10 концентрично розташованих доріжок (210 = 1024 > 1000). Зчитування інформації з фотодатчиків проходить у вигляді сигналів коду Грея або двійково-десяткового коду за один такт. На схемі прямокутниками позначено розташування фотоелементів 1, 2 і 3 для отримання двійкового коду. Код Грея часто будується з використанням кодової маски двійкового коду. Для цього фотоелементи зсувають відносно лінії зчитування двійкового коду у бік його збільшення на відстань, що дорівнює половині кодової ділянки кожного розряду 4, 5 і 6. Можлива також реалізація вдвічі більшої у порівнянні з двійковим кодом кількості кодових комбінацій без збільшення розрядності кодової маски. Для цього використовують додатковий (n +1)-й чутливий елемент, який розташовується відносно світлочутливого елемента n -го розряду на відстані половини кодової ділянки у бік її зменшення на тій же n -й кодовій доріжці. Таке розташування фотоелементів дозволяє отримати чотирьохрозрядний код Грея на трирозрядному розверстуванні двійкового коду. Використання коду Грея в перетворювачах кутових і лінійних переміщень обумовлено тим, що вдається ліквідувати неоднозначність зчитування без збільшення кількості фотоелементів у порівнянні з іншими кодами і тим самим досягнути високої розв’язуючої здатності. Всі датчики з кодовими масками мають недоліки: жорсткі вимоги до допусків і відносно великий час перетворень. Циклічні датчики формують значення, що періодично повторюються. При цьому виміряний параметр перетворюється у часовий інтервал. Такі датчики звичайно складаються з двох пристроїв: точного і грубого відліку. Пристрої точного відліку багаторазово повторюють цикл виміру за один оберт, що вносить неоднозначність у вимірювання кута повороту вала двигуна. Для усунення неоднозначності і визначення абсолютного значення параметра використовують пристрій грубого відліку, який проводить підрахунок кількості повних циклів роботи датчика від нульової позначки. Знаходження кількості доріжок кодового датчика, щоб він працював із заданою точністю, складається із таких етапів: 1. Знаходиться кількість ділень шкали, що відповідає необхідній точності. 2. Знаходяться ступені двійкового числа, між якими знаходиться визначена кількість ділень. 3. Вибирається більша ступінь, яка дорівнює необхідній кількості доріжок. ПРИКЛАД. Знайти кількість доріжок кодового датчика, щоб він працював з точністю 0,02 %. 1. Знаходження кількості ділень шкали 1 % відповідає 100 діленням шкали 0,02 % потребує кількістьділень шкали у 1:0,02 разів більшу Кількість ділень становить 100 ´ (1:0,02) = 5000 2. Знаходження ступенів двійкового числа 212 = 4096 < 5000< 213 = 8192 3. Відповідь: при зчитуванні інформації у двійковому коді мінімальна кількість доріжок становить 13, при зчитуванні інформації у коді Грея мінімальна кількість доріжок становить 12.
7 Методика виконання завдання № 7 [5]
ВИЗНАЧИТИ СТІЙКІСТЬ СИСТЕМИ ЗА ЗАДАНИМ ХАРАКТЕРИСТИЧНИМ РІВНЯННЯМ
Під стійкістю системи розуміють спроможність системи відновлювати вихідний (або практично близький до нього) стан після будь-якого збурення, який приводить до відхилення параметрів системи від номінального значення (рис. 7.1, а). Поняття стійкість, як і поняття рівноваги, може відноситись як до нерухомого стану тіла або системи (стійкість положення) так і до стану руху (стійкий і нестійкий рух). Нейтрально стійкі динамічні системи характеризуються тим, що при порушенні первісного стійкого стану, система після зняття збурення не повертається до цього початкового стану, але і не віддаляється від нього (рис.7.1, в).
а б в
Рисунок 7.1. Фізична модель стійкості систем: а - стійка; б - нестійка; в - нейтрально стійка
Розрізнюють стійкість в “малому” і “великому” При певних умовах стійка в “малому” система може виявитись нестійкою в “великому”. Перехідний процес в АСР залежить як від властивостей самої системи, так і від виду збурення, і включає в себе дві складові – вільні коливання в системі х в (t), які визначаються початковими умовами і внутрішніми властивостями самої системи; вимушені коливання х вм (t), які визначаються впливом збурення. х (t) = х в(t) + х вм(t) (7.1) Оскільки стійка система після припинення дії збурення повертається до сталого стану, то математичною умовою стійкості є вираз Вільний рух системи описується характеристичним рівнянням а о рп + а 1 рп - 1 +...+ ап -1 р + ап = 0, (7.2) де а о > 0; р - комплексне число. Умови, при яких можна досліджувати залежність результатів рішення лінійної системи і стійкості в “малому” без ризику отримати невірну відповідь, були обґрунтовані А.М. Ляпуновим доказом наступних двох теорем: 1. Якщо всі корені характеристичного рівняння лініарізованої системи, мають від’ємні дійсні частини, то нелінійна система, так само як і лініарізована, буде стійка при малих відхиленнях незалежно від відкинутих при лініарізації рівняння членів другого і більш високих ступенів відхилення. 2. Якщо серед коренів характеристичного рівняння лініарізованої системи, є хоча б один корінь з додатною дійсною частиною, то нелінійна система, так само як і лініарізована, буде нестійкою незалежно від відкинутих при лініарізації рівняння членів другого і більш високих ступенів відхилення. Якщо серед коренів характеристичного рівняння лініарізованої системи, є хоча б один корінь з нульовим значенням дійсної частини або чисто уявні корені, а всі інші корені мають від’ємну дійсну частину, то визначити стійкість нелінійної системи за лініарізованим рівнянням не можна.
а б в
Рисунок 7.2. Стійкість лініарізованих систем: а - стійка; б - нестійка; в - нейтрально-стійка;
Вісь і - межа стійкості. В нейтрально-стійкої системі Існують правила, які дозволяють судити про стійкість АСР, не вирішуючи громіздке диференційне рівняння - критерії стійкості. Критерії стійкості підрозділяють на алгебраїчні і частотні. До перших відноситься критерій Рауса-Гурвиця, до других - критерії Михайлова і Найквиста.
|

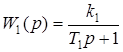 , а
, а  ; відповідно до (5.19) W 2(p) = е- p t; відповідно до (5.2) W 3(p) = k 2; відповідно до (5.10)
; відповідно до (5.19) W 2(p) = е- p t; відповідно до (5.2) W 3(p) = k 2; відповідно до (5.10)  . Передавальна функція складної системи дорівнює
. Передавальна функція складної системи дорівнює + k 2)/[1 + (
+ k 2)/[1 + ( ]. (5.27)
]. (5.27)
 аn 2cos nj -
аn 2cos nj -  (-1)n an 3cos n j. (6.5)
(-1)n an 3cos n j. (6.5) L = 2(a 1cosj + a 3co s 3j +...). (6.6)
L = 2(a 1cosj + a 3co s 3j +...). (6.6)



 . Таким чином, характер вільного руху системи визначає ступінь її стійкості. Оскільки вільний рух системи можна описати диференційним рівнянням, то і стійкість системи регулювання можна оцінити, вирішивши відповідне диференційне рівняння. Якщо стійкість системи регулювання можна оцінити за допомогою лінійних диференційних рівнянь, то її називають стійкістю в “малому”. Межі відхилення координат, у тому числі регульованої координати від положення рівноваги, в даному випадку не розглядаються, а ставлять лише умови достатньої малості цих відхилень.
. Таким чином, характер вільного руху системи визначає ступінь її стійкості. Оскільки вільний рух системи можна описати диференційним рівнянням, то і стійкість системи регулювання можна оцінити, вирішивши відповідне диференційне рівняння. Якщо стійкість системи регулювання можна оцінити за допомогою лінійних диференційних рівнянь, то її називають стійкістю в “малому”. Межі відхилення координат, у тому числі регульованої координати від положення рівноваги, в даному випадку не розглядаються, а ставлять лише умови достатньої малості цих відхилень.
 - корені характеристичного рівняння р 1 ... р 5
- корені характеристичного рівняння р 1 ... р 5 - прямує не до нуля, а до деякої постійної величини.
- прямує не до нуля, а до деякої постійної величини.


