Приведение сил и масс
Для упрощения расчётов механизм заменяют его динамической моделью – одним звеном, совершающим вращательное движение. Обычно это входное звено механизма. К нему приводятся все силовые и массовые характеристики:
Рисунок.1. Динамическая модель механизма.
Приведённые величины Угловая скорость звена приведения не постоянна, ввиду переменности приведённых величин. Его ускорение или замедление происходит вследствие неравенства приведённых моментов: движущего Ускорение звена приведения ε определяется в соответствии с известным выражением:
ε где:
Угловое ускорение вызывает и зменение угловой скорости звена приведения. Из выражения (6) видно, что все величины, кроме Увеличение постоянной составляющей приведённого момента инерции вызывает уменьшение углового ускорения ε, и, следовательно, уменьшение колебаний угловой скорости звена приведения. Маховик является элементом, который увеличивает постоянную составля-ющую
Определение приведённого момента
При определении приведённого момента внешних нагрузок
где:
Сумма мощностей сил
∑; Мощность силы определяется по значению (величине) силы, скорости точки её приложения и углу между векторами силы и скорости:
Произведение
Рисунок 2. К определению мощности силы.
Значение мощности силы с учётом масштаба плана скоростей равно:
Знак мощности определяется совпадением векторов F и VF – «плюс» или их противоположным направлением – «минус». Сумма мощностей моментов
Знак определяется совпадением направлений Следует обратить внимание, что силы инерции и моменты сил инерции не учитываются, так как они будут учтены в массовой характеристике звена приведения – приведённом моменте инерции
Определение приведённого момента инерции
При определении приведённого момента инерции условием эквивалентности является равенство кинетических энергий: звена приведения и всех звеньев механизма:
где:
Плоскопараллельное движение звена раскладывают на два простейших: поступательное движениес центром масс и вращательное относительно центра масс. Подсчёт значений приведённых моментов
Рисунок 3. Диаграмма приведённых моментов внешних нагрузок.
Рисунок 4. Диаграмма приведённых моментов инерции.
Приведённый момент инерции
где:
механизма, (переменная величина). Известно, что чем больше инерционность материальной системы, тем значительнее она сопротивляется изменению скорости при одинаковых внешних воздействиях. Обычно инерционность системы (механизма) увеличивают за счёт Если звено приведения обладает постоянным приведённым моментом инерции
Угловая скорость
Размах энергии за цикл равен:
Из полученного выражения определим
Таким образом, для обеспечения заданного коэффициента неравномерности Изменение кинетической энергии механизма происходит за счёт работы всех нагрузок (сил и моментов), приложенных к механизму (теорема об изменении кинетической энергии): ∆Т = ∑А, (17)
где ∆Т – изменение кинетической энергии; ∑А – сумма работ сил и моментов, приложенных к механизму.
Изменение кинетической энергии механизма ∆Т разделим на две части:
∆Т = ∆Т1 + ∆Т2, (18)
где ∆Т1 – изменение кинетической энергии з веньев с постоянным приведенным моментом инерции; ∆Т2 - изменение кинетической энергии звеньев с переменным приведенным моментом инерции.
Сумма работ состоит из работ движущих сил АД и приведённых работ сил сопротивления АП, поэтому:
откуда ∆Т1 учитывает изменение кинетической энергии звеньев с постоянным приведенным моментом инерции. К ним относятся: ротор двигателя, муфты, зубчатые колеса редуктора, ведущее звено механизма – звенья, совершающие непрерывные вращатель-ные движения в течение цикла. Эти звенья определяют постоянную составляющую кинетической энергии механизма и инерционность механизма, которая обеспечивает по-глощение или отдачу энергии, сглаживая неравномерность движения и выполняя частично роль МАХОВИКА. Если при этом неравномерность движения неудовлетво-рительна, то на одно из указанных звеньев (обычно – на входное звено, но желательна установка на звено с максимальной угловой скоростью) устанавливают дополнительный диск (маховик) с необходимым моментом инерции, определяемым расчетом. ∆Т2 учитывает изменение кинетической энергии звеньев с переменным приведенным моментом инерции – это все звенья механизма, совершающие прерывистые движения в течение цикла. Они увеличивают неравномерность движения наряду с другими факторами – переменными значениями сил сопротивления и движущих сил.
|

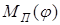 – приведённый момент внешних нагрузок – силовая характеристика;
– приведённый момент внешних нагрузок – силовая характеристика; – приведённый момент инерции – массовая характеристика;
– приведённый момент инерции – массовая характеристика; – приведённый момент движущих сил – силовая характеристика.
– приведённый момент движущих сил – силовая характеристика.
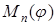 и
и  определяются из условий эквивалентности динамической модели и механизма.
определяются из условий эквивалентности динамической модели и механизма. и момента сил сопротивлений
и момента сил сопротивлений  . Кроме того, приведённый момент инерции
. Кроме того, приведённый момент инерции  – тоже переменная величина.
– тоже переменная величина. (6)
(6)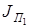 - постоянная составляющая приведённого момента инерции;
- постоянная составляющая приведённого момента инерции; - переменная составляющая приведённого момента инерции.
- переменная составляющая приведённого момента инерции. – переменные. С ними связано изменение углового ускорения ε.
– переменные. С ними связано изменение углового ускорения ε.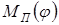 условием эквивалентности является равенство мощностей: приведённого момента и всех нагрузок, приложенных к механизму:
условием эквивалентности является равенство мощностей: приведённого момента и всех нагрузок, приложенных к механизму: ,(7)
,(7) – мощность приведённого момента;
– мощность приведённого момента; – сумма мощностей сил, приложенных к механизму;
– сумма мощностей сил, приложенных к механизму;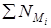 – сумма мощностей моментов, приложенных к механизму.
– сумма мощностей моментов, приложенных к механизму.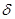 Ai = 0; ∑;
Ai = 0; ∑;  .
. есть проекция скорости на направление силы. Обозначим этот отрезок
есть проекция скорости на направление силы. Обозначим этот отрезок  F.
F.
 . (9)
. (9)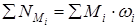 . (9)
. (9)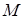 и
и  – «плюс», либо противоположным направлением – «минус».
– «плюс», либо противоположным направлением – «минус». (10)
(10) – массы звеньев, движущиеся поступательно;
– массы звеньев, движущиеся поступательно; – скорости центров масс звеньев;
– скорости центров масс звеньев; – моменты инерции вращающихся звеньев;
– моменты инерции вращающихся звеньев; – угловые скорости вращающихся звеньев.
– угловые скорости вращающихся звеньев.


 ,(11)
,(11) . Его величину подбирают такой, чтобы неравномерность движения, определяемая коэффициентом неравномерности
. Его величину подбирают такой, чтобы неравномерность движения, определяемая коэффициентом неравномерности  , была бы не более допустимой величины, которая задаётся в условиях для расчёта.
, была бы не более допустимой величины, которая задаётся в условиях для расчёта. равна:
равна: . (12)
. (12) до
до  , поэтому кинетическая энергия соответственно принимает максимальное и минимальное значение внутри цикла:
, поэтому кинетическая энергия соответственно принимает максимальное и минимальное значение внутри цикла: ,(13)
,(13) . (14)
. (14) (15)
(15) . (16)
. (16)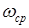 звена приведения и известном размахе кинетической энергии ∆Т
звена приведения и известном размахе кинетической энергии ∆Т  требуется постоянная составляющая момента инерции JП1, определяемая выражением (16).
требуется постоянная составляющая момента инерции JП1, определяемая выражением (16). ,
,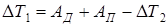 . (19)
. (19)


