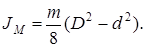Момент инерции маховика определяют по формуле (16), где в знаменателе задан-ные для расчета величины, а в числителе – размах кинетической энергии звеньев с постоянным приведенным моментом инерции. Если не учитывать ротор двигателя, муфты, зуб-чатые колеса редуктора, то ∆Т1 – размах кинетической энергии маховика.
Определение  начинают с построения диаграммы приведённых моментов
начинают с построения диаграммы приведённых моментов 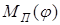 (рис. 5а). Графическим интегрированием этой диаграммы получают диаграмму приведённых работ
(рис. 5а). Графическим интегрированием этой диаграммы получают диаграмму приведённых работ 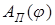 (рис. 5в). Соединив прямой начало координат диаграммы
(рис. 5в). Соединив прямой начало координат диаграммы 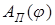 с её концом, получим диаграмму работ движущих сил
с её концом, получим диаграмму работ движущих сил  (рис. 5в), так как рассматривается период установившегося движения, когда не происходит изменения энергии за цикл: в конце цикла работы движущих сил и сил сопротивления равны. При этом предполагается, что момент двигателя – величина постоянная, поэтому его работа изобразится наклонной прямой на интегральной диаграмме.
(рис. 5в), так как рассматривается период установившегося движения, когда не происходит изменения энергии за цикл: в конце цикла работы движущих сил и сил сопротивления равны. При этом предполагается, что момент двигателя – величина постоянная, поэтому его работа изобразится наклонной прямой на интегральной диаграмме.
Следует иметь ввиду, что приведённый момент в технологических машинах 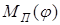 – в основном величина отрицательная и его работа
– в основном величина отрицательная и его работа 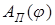 – тоже отрицательная величина, а работа движущих сил – величина положительная,но обе диаграммы расположены по одну сторону от оси абсцисс для удобства вычисления их суммы,называемой «избыточной энергией»,которая определяется ординатами диаграмм
– тоже отрицательная величина, а работа движущих сил – величина положительная,но обе диаграммы расположены по одну сторону от оси абсцисс для удобства вычисления их суммы,называемой «избыточной энергией»,которая определяется ординатами диаграмм 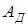 и
и  и их знаком. Если ордината
и их знаком. Если ордината  больше ординаты
больше ординаты 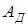 и обе расположены по одну сторону оси абсцисс, тогда их сумма отрицательна (ординаты вычитаются). При расположении диаграмм работ по разные стороны оси абсцисс – их сумма положительна (ординаты складываются).
и обе расположены по одну сторону оси абсцисс, тогда их сумма отрицательна (ординаты вычитаются). При расположении диаграмм работ по разные стороны оси абсцисс – их сумма положительна (ординаты складываются).
Затем строится диаграмма переменных приведённых моментов инерции  (рис. 5с). Она же будет являться диаграммой кинетической энергии звеньев с переменным приведённым моментом инерции
(рис. 5с). Она же будет являться диаграммой кинетической энергии звеньев с переменным приведённым моментом инерции  , если изменить масштаб оси ординат
, если изменить масштаб оси ординат  на
на  :
:

так как кинетическая энергия и момент инерции связаны такой же зависимостью (отличаются постоянным множителем):
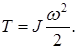
Затем (рис.5), согласно выражению (19) из суммы работ  вычитают кинетическую энергию звеньев
вычитают кинетическую энергию звеньев  и получают диаграмму кинетической энергии
и получают диаграмму кинетической энергии  . Для этого из разности ординат
. Для этого из разности ординат 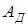 и
и  , умноженной на масштаб
, умноженной на масштаб 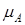 , вычитают значение ординаты
, вычитают значение ординаты  , умноженной на масштаб
, умноженной на масштаб  , и получают ординату диаграммы ∆Т1:
, и получают ординату диаграммы ∆Т1:

отсюда
 .
.
Получив 12 значений 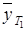 за цикл, строят диаграмму
за цикл, строят диаграмму  и определяют размах кинетической энергии
и определяют размах кинетической энергии  – отрезок
– отрезок  , необходимый для определения момента инерции маховика.
, необходимый для определения момента инерции маховика.

Рисунок 5. Определение 
Момент инерции 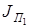 определяется по формуле (16):
определяется по формуле (16):
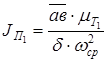 .
.
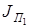 – это постоянная составляющая приведённого момента инерции. В нее входят моменты инерции: маховика, ротора двигателя, зубчатых колёс редуктора, муфт,самого звена приведения:
– это постоянная составляющая приведённого момента инерции. В нее входят моменты инерции: маховика, ротора двигателя, зубчатых колёс редуктора, муфт,самого звена приведения:
 .
.
Отсюда найдём момент инерции маховика  :
:
 ,
,
где:
 – момент инерции звена приведения;
– момент инерции звена приведения;
 – приведённый момент инерции ротора двигателя;
– приведённый момент инерции ротора двигателя;
 – приведённый момент инерции зубчатых колёс редуктора;
– приведённый момент инерции зубчатых колёс редуктора;
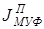 – приведённый момент инерции муфт.
– приведённый момент инерции муфт.
Приведённые моменты инерции указанных звеньев определяются из условий эквивалентности приводимой и приведённой величин – равенства их кинетических энергий. Например:
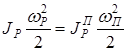 , откуда
, откуда  ;
;
соответственно:  ;
; 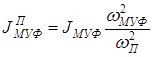 .
.
Здесь  – угловая скорость звена приведения. Нижние индексы означают: П – звено приведения; Р – ротор двигателя; МУФ – муфты; ЗК – зубчатые колеса. Верхний индекс П – признак приведенной величины. Отношения квадратов угловых скоростей можно заменить квадратом соответствующего передаточного отношения.
– угловая скорость звена приведения. Нижние индексы означают: П – звено приведения; Р – ротор двигателя; МУФ – муфты; ЗК – зубчатые колеса. Верхний индекс П – признак приведенной величины. Отношения квадратов угловых скоростей можно заменить квадратом соответствующего передаточного отношения.
После определения момента инерции маховика 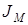 находят его ориентировочные размеры, представив маховик в виде кольца, у которого ширина
находят его ориентировочные размеры, представив маховик в виде кольца, у которого ширина 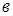 и высота
и высота  много меньше среднего диаметра
много меньше среднего диаметра 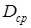 . В этом случае
. В этом случае 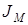 можно определить по формуле для точечной массы:
можно определить по формуле для точечной массы:
 .
.
Для кольца, изображённого на рис. 6, получим, заменив массу произведением объема кольца на плотность материала:

откуда  .
.
Величинами в и  задаются;
задаются;  - плотность материала.
- плотность материала.


Рисунок 6. К определению момента инерции маховика.
Если маховик будет выполнен в виде сплошного диска диаметром  и толщиной
и толщиной  , то нужно проинтегрировать элементарные моменты инерции от 0 до
, то нужно проинтегрировать элементарные моменты инерции от 0 до  :
:
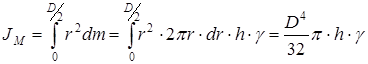 . (20)
. (20)

Рисунок 7. К определению момента инерции сплошного диска и кольца.
Если масса всего диска равна  , то её можно представить как объём диска, умноженный на плотность материала
, то её можно представить как объём диска, умноженный на плотность материала  :
:
 , (21)
, (21)
подставив (21) в (20), получим:
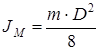 .
.
Если маховик является кольцом с внутренним диаметром 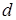 и наружным
и наружным  , то, интегрируя от
, то, интегрируя от 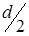 до
до  , получим:
, получим:
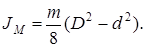

 начинают с построения диаграммы приведённых моментов
начинают с построения диаграммы приведённых моментов 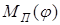 (рис. 5а). Графическим интегрированием этой диаграммы получают диаграмму приведённых работ
(рис. 5а). Графическим интегрированием этой диаграммы получают диаграмму приведённых работ 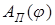 (рис. 5в). Соединив прямой начало координат диаграммы
(рис. 5в). Соединив прямой начало координат диаграммы  (рис. 5в), так как рассматривается период установившегося движения, когда не происходит изменения энергии за цикл: в конце цикла работы движущих сил и сил сопротивления равны. При этом предполагается, что момент двигателя – величина постоянная, поэтому его работа изобразится наклонной прямой на интегральной диаграмме.
(рис. 5в), так как рассматривается период установившегося движения, когда не происходит изменения энергии за цикл: в конце цикла работы движущих сил и сил сопротивления равны. При этом предполагается, что момент двигателя – величина постоянная, поэтому его работа изобразится наклонной прямой на интегральной диаграмме.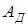 и
и  и их знаком. Если ордината
и их знаком. Если ордината  (рис. 5с). Она же будет являться диаграммой кинетической энергии звеньев с переменным приведённым моментом инерции
(рис. 5с). Она же будет являться диаграммой кинетической энергии звеньев с переменным приведённым моментом инерции  , если изменить масштаб оси ординат
, если изменить масштаб оси ординат  на
на  :
:
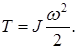
 вычитают кинетическую энергию звеньев
вычитают кинетическую энергию звеньев 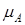 , вычитают значение ординаты
, вычитают значение ординаты  , и получают ординату диаграммы ∆Т1:
, и получают ординату диаграммы ∆Т1:
 .
.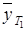 за цикл, строят диаграмму
за цикл, строят диаграмму  и определяют размах кинетической энергии
и определяют размах кинетической энергии  – отрезок
– отрезок  , необходимый для определения момента инерции маховика.
, необходимый для определения момента инерции маховика.

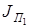 определяется по формуле (16):
определяется по формуле (16):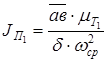 .
. .
. :
: ,
, – момент инерции звена приведения;
– момент инерции звена приведения; – приведённый момент инерции ротора двигателя;
– приведённый момент инерции ротора двигателя; – приведённый момент инерции зубчатых колёс редуктора;
– приведённый момент инерции зубчатых колёс редуктора;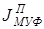 – приведённый момент инерции муфт.
– приведённый момент инерции муфт.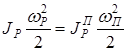 , откуда
, откуда  ;
; ;
; 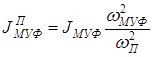 .
. – угловая скорость звена приведения. Нижние индексы означают: П – звено приведения; Р – ротор двигателя; МУФ – муфты; ЗК – зубчатые колеса. Верхний индекс П – признак приведенной величины. Отношения квадратов угловых скоростей можно заменить квадратом соответствующего передаточного отношения.
– угловая скорость звена приведения. Нижние индексы означают: П – звено приведения; Р – ротор двигателя; МУФ – муфты; ЗК – зубчатые колеса. Верхний индекс П – признак приведенной величины. Отношения квадратов угловых скоростей можно заменить квадратом соответствующего передаточного отношения.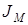 находят его ориентировочные размеры, представив маховик в виде кольца, у которого ширина
находят его ориентировочные размеры, представив маховик в виде кольца, у которого ширина 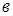 и высота
и высота  много меньше среднего диаметра
много меньше среднего диаметра 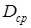 . В этом случае
. В этом случае  .
.
 .
. - плотность материала.
- плотность материала.

 и толщиной
и толщиной  :
: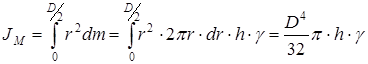 . (20)
. (20)
 , то её можно представить как объём диска, умноженный на плотность материала
, то её можно представить как объём диска, умноженный на плотность материала  , (21)
, (21)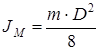 .
.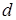 и наружным
и наружным 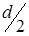 до
до