Пример расчета по методу Н.И. Мерцалова
Определить размеры обода маховика для механизма, изображенного на рис. 10. Известны размеры звеньев, их массы, моменты инерции, силы полезного сопротивления, угловая скорость входного звена Длины звеньев: Массы звеньев: Моменты инерции звеньев: Угловая скорость: Коэффициент неравномерности движения: Сила полезного сопротивления
Рисунок 10. Схема механизма,
Предварительно определим приведенный момент внешних нагрузок и приведенный момент инерции для заданного положения механизма. В курсовом проекте это выполня-ется для 12-и положений механизма. По полученным значениям строятся их диаграммы.
Определение приведённого момента внешних нагрузок
Приведённый момент внешних нагрузок определяется из условия эквивалентности: равенства мощностей приведённого момента и всех нагрузок, приложенных к механизму.
где Так как к механизму не приложены внешие моменты, то формула примет вид:
Вычислим приведённый момент
Результаты вычислений сводятся в таблицу 1.
Таблица 1. Определение приведённого момента внешних нагрузок.
Определение приведённого момента инерции Приведённый момент инерции определяется из условия эквивалентности – равенства кинетических энергий: звена приведения и всего механизма:
Для рассматриваемого механизма формула (31) примет вид:
Результаты вычислений и данные для расчётов сводятся в таблицу 2.
Таблица 2.
Первой строится диаграмма приведённых моментов внешних нагрузок
Рисунок11. Построение диаграммы кинетической энергии звеньев с постоянным приведённым моментом инерции.
Кинетическая энергия Δ Т1 определяется по известной зависимости (19):
Сумма работ Кинетическая энергия Определим
Найдем
Аналогично определяются кинетические энергии Построив диаграмму, найдем размах кинетической энергии
Определим момент инерции
Найдём средний диаметр обода маховика, представленного в виде кольца (рис. 6), не учитывая приведённые моменты ротора двигателя, самого звена приведения, зубчатых колёс редуктора, муфт. Если они известны, то их необходимо вычесть из полученного значения
Величинами в и
|

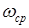 , коэффициент неравномерности движения
, коэффициент неравномерности движения  .
. мм,
мм,  мм,
мм,  мм;
мм; 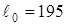 мм.
мм. кг,
кг,  кг,
кг, 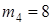 кг,
кг,  кг.
кг. кгм2,
кгм2,  кгм2,
кгм2,  кгм2.
кгм2. с-1.
с-1. .
. .
.
 и план скоростей,
и план скоростей, 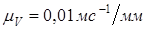 .
. .
. (30)
(30) – проекции скоростей на направл н ения сил.
– проекции скоростей на направл н ения сил. .
.








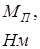
 .
. . (31)
. (31)
 кг
кг
 мм
мм
 кг
кг
 мм
мм
 кг
кг
 мм
мм
 кг
кг
 мм
мм
 мм
мм
 мм
мм
 кгм2
кгм2
 кгм2
кгм2
 мм
мм
 мм
мм
 кгм2
кгм2
 К определению приведённого момента инерции
К определению приведённого момента инерции  .
. . Под ней – диаграмма приведённых работ, которая получается в результате графического интегрирования диаграммы
. Под ней – диаграмма приведённых работ, которая получается в результате графического интегрирования диаграммы  . Под диаграммой работ располагается диаграмма приведённого момента инерции
. Под диаграммой работ располагается диаграмма приведённого момента инерции  и
и  ) кинетической энергии звеньев с переменным приведённым моментом инерции
) кинетической энергии звеньев с переменным приведённым моментом инерции  получают диаграмму кинетической энергии звеньев с постоянным приведённым моментом инерции
получают диаграмму кинетической энергии звеньев с постоянным приведённым моментом инерции  . По размаху энергии этой диаграммы
. По размаху энергии этой диаграммы 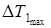 находят момент инерции маховика по формуле (16).
находят момент инерции маховика по формуле (16).
 .
. в пятом положении механизма определяется ординатой
в пятом положении механизма определяется ординатой  , причём она отрицательна, так как приведённые работы внешних нагрузок больше приведенных работ движущих сил (рис. 11в).
, причём она отрицательна, так как приведённые работы внешних нагрузок больше приведенных работ движущих сил (рис. 11в). (рис. 11с). Эти ординаты всегда положительны. Кинетическая энергия не может быть отрицательной.
(рис. 11с). Эти ординаты всегда положительны. Кинетическая энергия не может быть отрицательной. Дж.
Дж.
 (рис. 11d).
(рис. 11d). Дж.
Дж. :
: кгм2.
кгм2. = 0,01кгм2. По сравнению с
= 0,01кгм2. По сравнению с  м (439мм).
м (439мм). задаются. В расчете принято: в = 100 мм,
задаются. В расчете принято: в = 100 мм, 


