Синтез регулятора методом модального управління
| №
| Запитання та варіанти відповіді
| |
| В чому полягає задача модального управління (ЗМУ)?
Відповідь:
а) розрахувати параметри регулятора, які забезпечують задану частотну характеристику (ЧХ) системи автоматичного управління (САУ)
б) розрахувати параметри регулятора, які забезпечують задане розташування коренів характеристичного поліному (ХП) САУ
в) розрахувати параметри САУ, які забезпечують задане розташування коренів ХП САУ
г) розрахувати параметри регулятора, які забезпечують задану тривалість перехідного процесу
| |
| Як в матричному вигляді описується об’єкт управління (ОУ) в ЗМУ?
Відповідь:
а)  , де , де  - вхідний вектор ОУ, - вхідний вектор ОУ,  - вихід ОУ, - вихід ОУ, 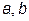 - матриці
б) - матриці
б)  , де , де  - вихідний вектор ОУ, - вихідний вектор ОУ,  - вхід ОУ, - вхід ОУ, 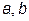 - матриці
в) - матриці
в)  , де , де  - вихідна величина регулятора, - вихідна величина регулятора,  - вхід ОУ, - вхід ОУ, 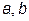 - матриці
г) - матриці
г)  , де , де  - вихідний вектор ОУ, - вихідний вектор ОУ,  - вхід ОУ, - вхід ОУ, 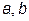 - матриці - матриці
| |
| Як описується регулятор в ЗМУ?
Відповідь:
а) u=[k1, k2,..kn]·(yg-y), де k1, k2,..kn – коефіцієнти регулятора; yg,, y - задане і фактичне значення виходу вимірювального пристрою, u – вхідний сигнал регулятора
б) u=[k1, k2,..kn]· y, де k1, k2,..kn – коефіцієнти регулятора; y - фактичне значення виходу вимірювального пристрою, u – вихідний сигнал регулятора
в) u=[k1, k2,..kn]·yg де k1, k2,..kn – коефіцієнти регулятора; yg, - задане значення виходу вимірювального пристрою, u – вихідний сигнал регулятора
г) u=[k1, k2,..kn]·(yg-y), де k1, k2,..kn – коефіцієнти регулятора; yg, y - задане і фактичне значення виходу вимірювального пристрою, u – вихідний сигнал регулятора
| |
| Які величини необхідні для розв’язку ЗМУ?
Відповідь:
а) n*n матриці a, c; n*n матриця b, n - вимірний вектор бажаних коренів ХП,значення n
б) n*n матриці a, c; n*1 матриця b, n - вимірний вектор бажаних коренів ХП
в) n*1 матриці a, c; n*n матриця b, n - вимірний вектор бажаних коренів ХП,значення n
г) n*n матриці a, c; n*1 матриця b, n - вимірний вектор бажаних коренів ХП,значення n
| |
| Яка умова однозначного розв’язку ЗМУ?
Відповідь:
а) вимірювальний пристрій (y=Cx) визначає всі координати вектора стану регулятора, вихід регулятора – векторна величина розмірності 2
б) вимірювальний пристрій визначає всі координати вектора стану ОУ, вихід регулятора – векторна величина розмірності 3
в) вимірювальний пристрій (y=Cx) визначає всі координати вектора стану ОУ, вихід регулятора – скалярна величина
г) вимірювальний пристрій визначає дві координати вектора стану ОУ, вихід регулятора – скалярна величина
| |
| Скільки передатних функцій (ПФ) необхідно визначити для розв’язку ЗМУ, у якій ОУ має порядок 4?
Відповідь:
а) 1
б) 2
в) 8
г) 4
| |
| Як визначається знаменник ПФ f(s) з матриці а, яка описує ОУ?
Відповідь:
а) f(s)=det(a)
б) f(s)=det(a-sE), де E - косодіагональна матриця
в) f(s)=det(a-sE), де E - симетрична матриця
г) f(s)=det(a-sE), де E - одинична матриця
| |
| Який вигляд має векторна ПФ ОУ x(s)/u(s) на першому етапі розв’язку ЗМУ?
Відповідь:
а) x(s)/u(s)= G·[1 s s2 .. sn-1]T/f(s), де рядки матриці G – це коефіцієнти чисельників n окремих ПФ ОУ (x1/u, x2/u,…,xn/u) в порядку зростання степені, а f(s) – ХП ОУ
б) x(s)/u(s)= G·[1 s s2 .. sn-1]T/f(s), де стовпці матриці G – це коефіцієнти чисельників n окремих ПФ ОУ (x1/u, x2/u,…, xn/u) в порядку зростання степені
в) x(s)/u(s)= G·[1 s s2 .. sn-1]T/f(s), де рядки матриці G – це коефіцієнти знаменників n окремих ПФ ОУ (x1/u, x2/u,…,xn/u) в порядку зростання степені, а f(s) – ХП ОУ
г) x(s)/u(s)= G·[1 s s2..sn-1]T/u(s), де рядки матриці G – це коефіцієнти чисельників n окремих ПФ ОУ (x1/u, x2/u,…,xn/u) в порядку зростання степені
| |
| Який знаходяться коефіцієнти бажаного ХП САУ h1, h2,…, hn?
Відповідь:
а) згідно теореми Безу: h1+h2s+h3s2+…+hnsn-1+sn=(s-s1)(s-s2)…(s-sn)
б) згідно теореми Безу: h1+h2s+h3s2+…+hnsn-1 =(s-s1)(s-s2)…(s-sn)
в) згідно теореми Безу: h1+h2s2+h3s3+…+hnsn+sn=(s-s1)(s-s2)…(s-sn)
г) згідно теореми Безу: h1+h2s+h3s2+…+hnsn-1+sn=(s-s1)(s-s2)…(s-sn-1)
| |
| Як у матричному вигляді записати рівняння розв’язку ЗМУ?
Відповідь:
а) (CG)T·kT=(h-f) , C- матриця вимірювального пристрою, G - матриця коефіцієнтів чисельників ПФ ОУ, k - коефіцієнти регулятора; h, f вектори коефіцієнтів бажаного ХП і коефіцієнтів ХП ОУ (k, h, f – вектори – рядки)
б) (CG)T·kT=(h-f)T , C- матриця вимірювального пристрою, G - матриця коефіцієнтів чисельників ПФ ОУ, k - коефіцієнти регулятора; h, f вектори коефіцієнтів бажаного ХП і коефіцієнтів ХП ОУ (k, h, f – вектори – рядки)
в) (CG)T·k=(h-f)T , C- матриця вимірювального пристрою, G - матриця коефіцієнтів чисельників ПФ ОУ, k - коефіцієнти регулятора; h, f вектори коефіцієнтів бажаного ХП і коефіцієнтів ХП ОУ(k, h, f – вектори – рядки)
г) (CG)T·kT=(h-f)T , C- матриця ОУ, G - матриця коефіцієнтів чисельників ПФ ОУ, k - коефіцієнти регулятора; h, f вектори коефіцієнтів бажаного ХП і коефіцієнтів ХП ОУ (k, h, f – вектори – рядки)
| |
| Чому дорівнюють коефіцієнти бажаного ХП САУ в порядку зростання степені, коли задані корені:
-2, -3+5j, -3-5j?
Відповідь:
а) 89, 54, 10
б) 68, 46, 8
в) 87, 56, 8
г) 96, 40, 4
| |
| Для чого введена допоміжна підпрограма у підпрограмі mod розв’язку ЗМУ?
Відповідь:
а) для того щоб узгодити проміжні двовимірні масиви, які не входять у список формальних аргументів підпрограми mod, з розмірами матриць a та b, які описують вимірювальний пристрій
б) для того щоб узгодити проміжні масиви, які не входять у список аргументів підпрограми mod, з розмірами матриць a та b, які описують ОУ
в) для того щоб узгодити проміжні двовимірні масиви, які не входять у список формальних аргументів підпрограми mod, з розмірами матриць a та b, які описують ОУ
г) для того щоб узгодити проміжні двовимірні масиви, які входять у список формальних аргументів підпрограми mod, з розмірами матриць a та b, які описують ОУ
| |
| Чому дорівнює коефіцієнт регулятора кр, який забезпечує корінь ХП замкнутої САУ s1=-α, якщо ОУ являє собою аперіодичну ланку з параметрами k, T (α>1/T)?
Відповідь:
а) kp=(αT+1)/k
б) kp=(αT-1)/k
в) kp=(αT-1)/(2k)
г) kp=(α+T-1)/k
| |
| Які переваги і недоліки методу синтезу регулятора шляхом розв’язку ЗМУ?
Відповідь:
а) нескладний алгоритм розрахунків, забезпечує задані тривалість і характер перехідного процесу, але вимагає визначення всіх координат вектора стану ОУ, неоднозначний розв’язок, коли вихід регулятора – нелінійна величина, не враховується належним чином вигляд чисельника ПФ САУ
б) нескладний алгоритм розрахунків, забезпечує задані тривалість і характер перехідного процесу, але вимагає визначення всіх координат вектора стану ОУ, неоднозначний розв’язок, коли вихід регулятора – векторна величина, не враховується належним чином вигляд чисельника ПФ САУ
в) нескладний алгоритм розрахунків, забезпечує задані ЧХ і характер перехідного процесу, але вимагає визначення всіх координат вектора стану ОУ, неоднозначний розв’язок, коли вихід регулятора – векторна величина, не враховується належним чином вигляд чисельника ПФ САУ
г) нескладний алгоритм розрахунків, забезпечує задані тривалість і характер перехідного процесу, але вимагає визначення декількох координат вектора стану, неоднозначний розв’язок, коли вихід регулятора – трансцендентна величина, не враховується належним чином вигляд чисельника ПФ САУ
| |
| Синтез регулятора шляхом розв’язку ЗМУ є параметричним чи структурним і чому?
Відповідь:
а) кількість каналів регулятора залежить від порядку ОУ, тому регулятор не має жорсткої структури; отже цей спосіб синтезу є структурним
б) структура регулятора задана, розраховуються тільки його коефіцієнт підсилення; тому цей спосіб синтезу є параметричним
в) структура регулятора змінюється залежно від порядку ОУ, але, крім того, розраховуються його коефіцієнти підсилення в каналах, отже цей спосіб синтезу є структурно - параметричним
г) структура регулятора задана, розраховуються тільки його коефіцієнти підсилення в каналах, кількість яких дорівнює порядку ОУ; отже цей спосіб синтезу є параметричним
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...
Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...
Именные части речи, их общие и отличительные признаки Именные части речи в русском языке — это имя существительное, имя прилагательное, имя числительное, местоимение...
|
Методы анализа финансово-хозяйственной деятельности предприятия
Содержанием анализа финансово-хозяйственной деятельности предприятия является глубокое и всестороннее изучение экономической информации о функционировании анализируемого субъекта хозяйствования с целью принятия оптимальных управленческих...
Образование соседних чисел Фрагмент:
Программная задача: показать образование числа 4 и числа 3 друг из друга...
Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|
|