Розрахунок коренів ХП
| №
| Запитання та варіанти відповіді
| |
| Що називається коренем поліному 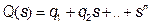 ?
Відповідь:
а) корінь поліному перетворює ?
Відповідь:
а) корінь поліному перетворює  в просте число, більше в просте число, більше 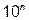 б) це таке значення змінної
б) це таке значення змінної 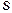 , коли , коли  наближається до нескінченності
в) значення змінної наближається до нескінченності
в) значення змінної 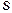 , що забезпечує виконання рівності , що забезпечує виконання рівності  г) значення змінної
г) значення змінної 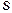 , що забезпечує виконання рівності , що забезпечує виконання рівності 
| |
| Що дає для аналізу САУ розрахунок коренів ХП?
Відповідь:
а) знаючи корені, можна визначити тривалість перехідного процесу, коли корені комплексні, то можна оцінити частоти коливальних складових і тривалість їх затухання
б) знаючи корені, можна визначити ступінь стійкості САУ, тривалість перехідного процесу і особливість його залежності від часу (аперіодичний чи коливальний); коли корені комплексні, то можна оцінити частоти коливальних складових і тривалість їх затухання
в) знаючи корені, можна визначити ступінь стійкості САУ і особливість залежності перехідного процесу від часу (аперіодичний чи коливальний); коли корені комплексні, то можна оцінити частоти коливальних складових і тривалість їх затухання
г) знаючи корені, можна визначити ступінь стійкості САУ, тривалість перехідного процесу; коли корені комплексні, то можна оцінити частоти коливальних складових і тривалість їх затухання
| |
| Чому дорівнює перше наближення квадратичного дільника (КД), який має корені з найбільшим модулем, коли відомі коефіцієнти полінома 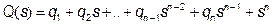 ?
Відповідь:
а) ?
Відповідь:
а)  б)
б)  в) s2+qns+1
г) s2+q2s+q1
в) s2+qns+1
г) s2+q2s+q1
| |
| Скільки разів має місце ділення на КД у методі Берстоу для його уточнення?
Відповідь:
а) 3
б) 4
в) 2
г) 1
| |
| Як покращити збіжність ітерацій уточнення КД полінома Q(s), що має корені з модулем більше одиниці, методом Лобачевського?
Відповідь:
а) в поліномі Q(s) поміняти знаки при непарних степенях s, до нового поліному Q1(s) додати Q(s), в результаті утвориться поліном F(s2)=Q+Q1, відстань між коренями якого зростає, що дає покращення збіжності ітерацій
б) в поліномі Q(s) поміняти знаки при непарних степенях s, новий поліном Q1(s) поділити на Q(s), в результаті утвориться поліном F(s2)=Q1/Q, відстань між коренями якого зростає, що дає покращення збіжності ітерацій
в) в поліномі Q(s) поміняти знаки при парних степенях s, новий поліном Q1(s) помножити на Q(s), в результаті утвориться поліном F(s2)=Q·Q1, відстань між коренями якого зростає, що дає покращення збіжності ітерацій
г) в поліномі Q(s) поміняти знаки при непарних степенях s, новий поліном Q1(s) помножити на Q(s), в результаті утвориться поліном F(s2)=Q·Q1, відстань між коренями якого зростає, що дає покращення збіжності ітерацій
| |
| Як зменшити порядок полінома Q(s) після визначення точного КД?
Відповідь:
а) поліном Q(s) поділити на КД, частка від цього ділення матиме порядок на 1 менший ніж Q(s)
б) до полінома Q(s) додати КД, результат поділити КД2, тоді порядок Q(s) зменшиться
в) поліном Q(s) помножити на КД, добуток матиме порядок на 2 менший ніж Q(s)
г) поліном Q(s) поділити на КД, частка від цього ділення матиме порядок на 2 менший ніж Q(s)
| |
| Яка послідовність дій для визначення коренів ХП Q(s)?
Відповідь:
а) визначити наближений КД, уточнити його, поділити Q на КД, порядок Q зменшиться на 3. Цей процес повторюється поки порядок Q більше 2, далі розв’язується рівняння 2-ї або 1-ї степені
б) визначити наближений КД, уточнити його і додати його до Q, порядок Q зменшиться на 2. Цей процес повторюється поки порядок Q більше 2, далі розв’язується рівняння 2-ї або 1-ї степені
в) визначити наближений КД, уточнити його, помножити Q на КД, порядок Q зменшиться на 2. Цей процес повторюється поки порядок Q більше 2, далі розв’язується рівняння 2-ї або 1-ї степені
г) визначити наближений КД, уточнити його, поділити Q на КД, порядок Q зменшиться на 2. Цей процес повторюється поки порядок Q більше 2, далі розв’язується рівняння 2-ї або 1-ї степені
| |
| Як перейти від коренів s1, s2,..,sn ХП Q(s)=q1+q2s+..+qnsn-1+sn до його коефіцієнтів q1, q2,..qn?
Відповідь:
а) використати теорему Безу Q=(s-s1)·(s-s2)·…·(s-sn)
б) використати теорему Безу Q=(s-s1)+(s-s2)+…+(s-sn)
в) використати залежність qi=sn-i, i=1, 2, … n
г) спираючись на значення коренів коефіцієнти ХП визначити ітераційним шляхом
| |
| Чому дорівнює остача від ділення полінома  на КД на КД  ?
Відповідь:
а) 0
б) 2
в) 4
г) 1.5 ?
Відповідь:
а) 0
б) 2
в) 4
г) 1.5
| |
| Чому дорівнює частка від ділення полінома  на КД на КД  ?
Відповідь:
а) s+1
б) s-1
в) s+2
г) s ?
Відповідь:
а) s+1
б) s-1
в) s+2
г) s
| |
| Чому дорівнює перше наближення КД з найбільшими модулями коренів, коли ХП Q(s)=s3+4s2+30s+52?
Відповідь:
а) s2+7.5s+13
б) s2+4s+30
в) s2+30s+13
г) s2+7.5s+26
| |
| Чому дорівнює перше наближення КД з найменшими модулями коренів, коли ХП Q(s)=s3+4s2+30s+52?
Відповідь:
а) s2+7.5s+26
б) s2+30s+13
в) s2+7.5s+13
г) s2+4s+30
| |
| Які вхідні та вихідні величини підпрограми ділення полінома q1+q2s+..+qnsn-1+qn+1sn на КД s2+ps+q?
Відповідь:
а) вхідні: n, q1,…, qn+1, p, q, вихідні: n-1 коефіцієнтів частки та 3 коефіцієнти залишку
б) вхідні: q1,…, qn+1, p, q, вихідні: n-1 коефіцієнтів частки та 2 коефіцієнти залишку
в) вхідні: n, q1,…, qn+1, p, q, вихідні: n коефіцієнтів частки та 2 коефіцієнти залишку
г) вхідні: n, q1,…, qn+1, p, q, вихідні: n-1 коефіцієнтів частки та 2 коефіцієнти залишку
| |
| Який порядок і тип системи алгебраїчних рівнянь для знаходження поправок коефіцієнтів КД у методі Берстоу?
Відповідь:
а) два лінійних диференційних рівняння
б) одне нелінійне алгебраїчне рівняння
в) два лінійних алгебраїчних рівняння
г) одне трансцендентне рівняння
| |
| Як визначити збіжність ітерацій уточнення КД методом Берстоу?
Відповідь:
а) величини коефіцієнтів від множення полінома на КД після кожної ітерації зменшуються
б) величини коефіцієнтів залишку від ділення полінома на КД після кожної ітерації не зростають
в) коефіцієнти залишку від ділення полінома на КД після кожної ітерації зменшуються
г) величини коефіцієнтів залишку від ділення полінома на КД після кожної ітерації зменшуються
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Пункты решения командира взвода на организацию боя. уяснение полученной задачи; оценка обстановки; принятие решения; проведение рекогносцировки; отдача боевого приказа; организация взаимодействия...
Что такое пропорции?
Это соотношение частей целого между собой. Что может являться частями в образе или в луке...
Растягивание костей и хрящей. Данные способы применимы в случае закрытых зон роста.
Врачи-хирурги выяснили...
|
Различия в философии античности, средневековья и Возрождения ♦Венцом античной философии было: Единое Благо, Мировой Ум, Мировая Душа, Космос...
Характерные черты немецкой классической философии 1. Особое понимание роли философии в истории человечества, в развитии мировой культуры. Классические немецкие философы полагали, что философия призвана быть критической совестью культуры, «душой» культуры.
2. Исследовались не только человеческая...
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит...
|
|