Задача о назначениях
Задача состоит в том, что требуется найти такое множество назначений i-х исполнителей (претендентов) на j-е работы Kij (i=1,2,...,n; j=1,2,...n), при которых достигается максимум эффекта
и выполняются ограничения
1, если i-й объект назначен на j-ю работу Kij= 0, в противном случае. Задача решается венгерским методом или как транспортная задача линейного программирования, но на максимум целевой функции.
118. Алгоритм метода ближайшего соседа (один из вариантов): 1) создается рабочий массив 2) текущее множество перемещений коммивояжера L задается нулевым (число переходов m=0). В итоге решения элементы массива L будут представлять перечень пунктов lk, k=1,2,…,m (m=n+1); 3) находится звено максимальной стоимости из массива 4) изменяется m (m=m+1) и один из пунктов r или s, например, пункт r вводится во множество L (lm=l1=r); 5) составляется путь перемещений коммивояжера: 5.1) рассматривается множество M звеньев массива, соединенных с пунктами l1 и lm (т.е. рассматриваются звенья 5.2) находится звено минимальной стоимости из массива М как 5.3) изменяется m (m=m+1); 5.4) текущее множество перемещений коммивояжера L дополняется звеном rs. Если l1=r, то lk=lk-1, k=m, m-1,...,2 и l1= s, а если lm-1=r, то lm= s; 5.5) заменяются элементы 5.6) если l1 = lm-1 , то переход на пункт 6 и если иначе, то заменяются элементы 5.7) если l2= r, то 6) возврат на 5.1. 7) контур перемещений замыкается путем введения еще одного перехода (m=m+1 и lm= l1). 119. Алгоритм простейшей реализации метода ветвей и границ следующий: 1) принимается один из пунктов за начальный пункт ветвления, например, один из пунктов, принадлежащих звену (переходу) с наибольшей стоимостью (длиной). Стоимость (длина) ветвления у начального пункта принимается равной нулю; 2) из пункта с минимальной стоимостью ветвления (минимальной текущей оценкой границы ветвления) производятся ветвления (включение звеньев переходов), не дающие замкнутого цикла (в ветви отсутствуют пункты с одинаковыми номерами кроме последнего n-го шага ветвления по каждой ветви) и рассчитываются стоимости ветвления у вновь включенных в ветви пунктов; каждая ветвь на n-м шаге замыкается на начальный пункт. Стоимость у вновь включенных в ветвление пунктов рассчитывается по формуле Zji=Zj,i -1 + ci, где Zji и Zj,i-1– соответственно оценка стоимости j-й ветви на шаге i и i-1;ci – стоимость звена (перехода), включаемого в ветвь на i-м шаге; 3) находится минимальное значение из всех рассчитанных стоимостей дерева ветвления. Если какая-то ветвь имеет число переходов (звеньев) n и минимальное значение стоимости ветвления, то оптимальное решение получено, а иначе необходимо продолжать ветвление (переход на п. 2). Одна из ветвей с минимальным значением стоимости ветвления у конечного пункта и включающая все n пунктов, дает решение. 120. Имеется n пунктов, в которых должен побывать коммивояжер. Задана матрица стоимостей (расстояний, времени и т.п.) на переход между пунктами cij , i=1,2,...,n и j=1,2,...,n. Коммивояжер должен выйти из одного из пунктов, побывать во всех остальных пунктах по одному разу и вернуться в начальный пункт. Необходимо найти порядок обхода, дающий минимальную суммарную стоимость посещения всех пунктов. Введем переменную Kjj Kij = 1, при переходе между пунктами i и j, 0, если нет перехода между пунктами i и j Необходимо найти множество {Kij }, i=1,2,...,n и j=1,2,...,n, дающее минимум
и выполнение ограничений
Ui -Uj +nK ij £ n-1, i ¹ j, (***) где Ui, Uj – целые неотрицательные числа, представляющие собой номер этапа, на котором посещается пункт. Условие (*) означает, что коммивояжер выходит из каждого пункта один раз, а условие (**) – что он входит в каждый пункт только один раз. Условие (***) обеспечивает замкнутость цикла (контура) только на n-м этапе решения задачи. Задача без учета условия (***), представляет постановку, аналогичную задаче о назначениях и отличается тем, что целевая функция стремится к минимуму (Z→min). Если при ее решении получен замкнутый контур, то это оптимальное решение, а иначе полученное значение целевой функции является той оценкой, которая всегда меньше или равна целевой функции (длине пути) с учетом условия (***). Точное решение задачи дает метод ветвей и границ, а приближенные – метод ближайшего соседа, метод сумм (изложен ранее для составления сборочно-развозочных маршрутов), метод Кларка-Райта.
|


 , j=1,n;
, j=1,n; , i=1,n;
, i=1,n; , i=1, 2,...,n; j=1, 2,..., n;
, i=1, 2,...,n; j=1, 2,..., n; как
как  (i¹j);
(i¹j); и
и  );
); . Если crs=1Е12, то решение закончено (переход на 7). Иначе переход на 5.3;
. Если crs=1Е12, то решение закончено (переход на 7). Иначе переход на 5.3; =
=  = 1Е12;
= 1Е12; =
= 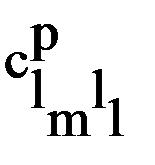 = 1Е12;
= 1Е12;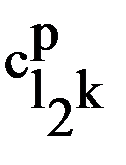 =
=  = 1Е12, k= 1, 2,..., n или если lm-1=r, то
= 1Е12, k= 1, 2,..., n или если lm-1=r, то  =
=  = 1Е12, k=1,2,...,n;
= 1Е12, k=1,2,...,n;
 ; (*)
; (*) ; (**)
; (**)


