Транспортная задача линейного программирования
Ряд задач оперативного управления сводятся к решению задачи оптимального закрепления потребителей за поставщиками, состоящей в определении наилучшего плана поставок однородных (взаимозаменяемых) ресурсов (грузов, автомобилей и т.п.) от m поставщиков Ai ( Задача оптимизации закрепления потребителей за поставщиками применяется при оптимизации грузопотоков (грузоотправители – поставщики, грузополучатели – потребители), возврата порожних транспортных средств (грузополучатели – поставщики порожних транспортных средств, грузоотправители – получатели порожних транспортных средств), подачи транспортных средств в начальные пункты маршрутов (предприятия-перевозчики – поставщики, начальные пункты маршрутов – получатели транспортных средств). Первая задача – получить грузопотоки, обеспечивающие минимальный грузооборот; вторая и третья – обеспечить минимум непроизводительных перемещений транспортных средств. Таблица 3.3 – Распределительная таблица (общий вид)
63.Отыскание кратчайшей связывающей сети Кратчайшая связывающая сеть (КСС) представляет собой "дерево" графа минимальной длины, т.е. она не должна содержать контуров (циклов) и включать звенья, которые дают суммарную минимальную длину. Применяется для нахождения сети маршрутов минимальной длины, соединяющей заданные пункты (маршруты перевозок пассажиров или мелких партий грузов, сеть путей с определенными свойствами и т.п.). Один из алгоритмов отыскания кратчайшей связывающей сети следующий: 1) находится звено минимальной длины и включается в КСС; 2) последовательно включаются звенья в КСС: 2.1) находятся звенья, соединенные только одним своим концом с имеющейся частью КСС. Если нет ни одного такого звена, то решение закончено. Иначе переход на следующий пункт 2.2; 2.2) из найденных по п. 2.1 звеньев определяется звено минимальной длины и включается в КСС; 2.3) переход на 2.1. Кратчайшая связывающая сеть включает ровно m-1 звеньев при числе вершин m.
Пример. Необходимо найти кратчайшую связывающую сеть для ранее приведенной схемы транспортной сети.
Решение. 1) находим из всех звеньев звено минимальной длины и включаем в КСС сеть (звено 3-4); 2) последовательно включаем звенья в КСС: 1-итерация 2.1.1) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Это звенья 3-2, 4-2 и 4-5. 2.2.1) из выбранных звеньев находим звено минимальной длины и включаем в КСС. Это звено 4-5; 2.3.1) переход на 2.1.2. 2- итерация 2.1.2) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Это звенья 3-2, 4-2 и 5-1. 2.2.2) из выбранных звеньев находим звено минимальной длины и включаем в КСС. Поскольку все звенья равной минимальной длины, то выбираем любое из них, например звено 5 - 1; 2.3.2) переход на 2.1.3. 3- итерация 2.1.3) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Это звенья 3-2, 4-2 и 1-2. 2.2.3) из выбранных звеньев находим звено минимальной длины и включаем в КСС. Это звено 1-2; переход на 2.1.4. 4- итерация 2.1.4) выбираем звенья, соединенные только одним своим концом с имеющейся частью КСС. Таких звеньев нет. Решение закончено. Звенья КСС выделены линиями большей толщины (рисунок 3.22). Пуск
2
Ввод n, ip n – число вершин транспортной сети ip – признак одностороннего движения (0 – нет, 1 – да);
3 5 ip=1 Нет Ввод sij, sij –длина звеньев (вводится
Да 4 6 sij, sji =sji,
sij=0, i = j
8 16 sij –расстояние между пунктами i и j
9 17
10 Да Sjk k sj i > 1E19 Sik j Sji i
Нет
Да 12 Нет 13 s i k > 1E19 c = s ji + s i k
15 Да 14 s j k = c c < s jk p j k = i
Нет Рисунок 3.21 – Алгоритм метода поиска кратчайших расстояний между пунктами транспортной сети
2
6км
5км 6 км 3 км
1 4
5 км 6 км
Рисунок 3.22 – Схема кратчайшей связывающей сети (жирные линии) 64.Звено транспортной сети и его параметры Транспортная сеть района (региона) представляет собой систему путей сообщения, предназначенную для передвижения транспортных средств. Модель транспортной сети – это описание местонахождения ее вершин (пунктов), а также длин и других параметров (характеристик) соединяющих вершины звеньев. Может быть задана в графическом или табличном виде. Звеном транспортной сети является ее часть, соединяющая две смежные вершины. Длина звеньев может быть выражена в единицах длины, приведенных километрах, единицах времени, стоимостном измерении и т.п. (в дальнейшем длина). В качестве других параметров звеньев может быть задана техническая категория пути сообщения и др. Вершины (пункты) транспортной сети соответствуют местонахождению ресурсообразующих и ресурсопоглащающих точек, терминалов, пересечений путей. Длина звеньев транспортной сети определяется по справочным таблицам, атласам дорог, с помощью курвиметра по масштабным картам и планам, а также непосредственным замером на местности, например по показаниям одометра (счетчика пройденного пути) автомобиля.
65.Постановка транспортной задачи линейного программирования с дополнительными условиями
При наличии ограничений на размер корреспонденций, задача в дальнейшем решается по следующей схеме: 1) проверяется выполнение условия Xij £Xoij для связей ij. Если условие выполняется для всех связей, то решение закончено (переход на блок 10 общего алгоритма), иначе переход на пункт 2; 2) для каждой связи ij, по которой имеет место условие Xij > Xoij , последовательно должен быть реализован алгоритм: 2.1) в окончательное решение вводится корреспонденция Xij = Xoij ; 2.2) корректируются соответствующие размеры наличия и потребности в ресурсе XА j =XА j - Xij ; XBj = XBj - Xij ; 2.3) корректируется соответствующая стоимость поставки lij путем замены на большое число, например 3) переход на блок 4 укрупненного алгоритма решения задачи. Решение задачи с запрещением поставки ресурса от i-го поставщика j-му потребителю решается по общей схеме с предварительной заменой реальной стоимости lij на большое число, например Решение задачи с необходимостью обеспечения поставки от i-го поставщика j-му потребителю в гарантированном объеме Xгij производится следующим образом: 1) предварительно для каждой такой связи ij, по которой имеет место условие Xij³Xгij: 1.1) в окончательное решение вводится корреспонденция Xij=Xгij; 1.2) корректируются соответствующие размеры наличия и потребности в ресурсе XАj=XАj-Xij; XBj=XBj-Xij; 2) решается задача с новыми условиями по общей схеме. Полное окончательное решение будет представлять собой множество корреспонденций, полученных решением по измененным условиям, и корреспонденций, назначенных по пункту 1.1). При решении несбалансированной транспортной задачи возможно за счет назначения различных стоимостей по фиктивному пункту распределение по какому-то из пунктов корреспонденции реального или фиктивного ресурса. Так, если по одному из пунктов в корреспонденции с фиктивным поставить относительно большее значение стоимости, то это явится предпосылкой, что по нему будет назначена корреспонденция только реального ресурса (по пункту будет обеспечена поставка реального ресурса). Наоборот, если поставить относительно меньшее значение стоимости, то это вызовет назначение корреспонденции в виде фиктивного ресурса (не будет обеспечена поставка реального ресурса). При одинаковом значении стоимости в корреспонденции с фиктивным пунктом фиктивные поставки будут назначены исходя из минимума общих затрат на поставки, что не всегда отвечает реальным требованиям производства. Компьютерная программа решения транспортной задачи линейного программирования приведена в приложении 8. Программа состоит из головного модуля, модуля ввода данных и модуля выполнения расчетов.
66.Реализация симплекс-метода для задачи линейного программирования, приведенной к стандартному виду Для применения симплекс-метода исходные данные задачи приводят к каноническому (стандартному) виду путем ввода дополнительных переменных по числу ограничений типа неравенств из общего числа n. Цель – заменить ограничения типа неравенств ограничениями типа равенств. Стандартная форма задачи имеет вид: целевая функция
ci = 0 для ограничения
где M = m+n и
Для неравенств типа £ dij=1 и для типа ³ dij= - 1. Например, стандартная форма для ранее приведенной задачи следующая: 20 x1+ 25 x2 + 1 x3+ 0 x4 = 175 x1 + x2 + 0 x1+ 1 x2 = 8 Z = 5 x1+ 6 x2 + 0 x3+ 0 x4 = max.
Основные шаги решения задачи (после представления исходной системы в стандартном виде): 1) формируется первоначальное базисное решение; 2) выражается Z через небазисные переменные; 3) проверяется базисное решение на оптимальность. Если оптимально, то на п.10; 4) проверяется задача на наличие решения. Если решения нет, то выход; 5) выбирается из небазисных переменных та, которая способна при введении ее в базис в большей степени улучшить значение целевой функции, и вводится в базис; 6) определяется базисная переменная, которая выводится из базиса; 7) алгебраически выражается вводимая в базис переменная через переменную, выводимую из базиса и другие небазисные переменные; 8) алгебраически выражаются другие базисные переменные через небазисные; 9) переход на п. 2; 10) определяются значения базисных переменных. Они являются решением задачи. Итерационный процесс (шаги 2–9) повторяются до тех пор, пока не произойдет выход на шаге 3 или 4. Алгоритм реализации отдельных шагов при решении задачи на максимум и ограничениях типа £ следующий:
67.Постановка транспортной задачи линейного программирования без дополнительных условий
Ряд задач оперативного управления сводятся к решению задачи оптимального закрепления потребителей за поставщиками, состоящей в определении наилучшего плана поставок однородных (взаимозаменяемых) ресурсов (грузов, автомобилей и т.п.) от m поставщиков Ai ( Задача оптимизации закрепления потребителей за поставщиками применяется при оптимизации грузопотоков (грузоотправители – поставщики, грузополучатели – потребители), возврата порожних транспортных средств (грузополучатели – поставщики порожних транспортных средств, грузоотправители – получатели порожних транспортных средств), подачи транспортных средств в начальные пункты маршрутов (предприятия-перевозчики – поставщики, начальные пункты маршрутов – получатели транспортных средств). Первая задача – получить грузопотоки, обеспечивающие минимальный грузооборот; вторая и третья – обеспечить минимум непроизводительных перемещений транспортных средств. На основании полученных оптимальных планов закрепления потребителей ресурса за поставщиками может строиться картограмма поставок. Для этого эпюры потоков ресурса накладываются на схему транспортной сети. При построении необходимо учитывать, что ресурс корреспондирует по пути с минимальной стоимостью перемещения (кратчайшему пути) между пунктами i и j транспортной сети. Если обозначить размер ресурса (вывоза) от поставщика Ai через XAi, требуемый размер поставки потребителю Bj через XBj, размер корреспонденции от i-го поставщика j-му получателю (потребителю) через Xij и стоимость поставки единицы ресурса между ними через lij, то поставленная задача в математической форме примет вид:
Xij ³ 0. (3.4) В случае, если запасы у поставщиков равны общим потребностям получателей, то
Поставленная таким образом задача (ограничения 3.1, 3.2, 3.4 и целевая функция 3.3) является сбалансированной моделью (условие 3.5) классической транспортной задачи линейного программирования, в результате решения которой по известным значениям XAi, XBj, lij находятся оптимальные значения корреспонденций Xij. Задача может быть поставлена с дополнительными условиями: 1) имеются ограничения на размер поставок от каждого i-го поставщика каждому j-му потребителю в объемах Xоij, 2) запрещена поставка ресурса от i-го поставщика j-му потребителю, т.е. должно быть обеспечено условие Xij=0; 3) должна быть обеспечена поставка от i-го поставщика j-му потребителю в гарантированном объеме Xгij (Xгij ≤ XАi и Xгij ≤ XВj ); 4) при несбалансированной задаче необходимо назначить по какому-то из пунктов корреспонденцию реального или фиктивного ресурса. Для решения транспортная задача может быть представлена в виде распределительной таблицы (таблица 3.23). Общий алгоритм решения несбалансированной задачи с учетом ограничений на размер корреспонденций представлен на рисунке 3.23. 68.Поиск оптимума одномерной дифференцируемой функции Унимодальной называется функция, имеющая один экстремум. Задача поиска экстремума сводится к нахождению значения хо, соответствующего максимуму или минимуму f(x). Алгоритм численного метода или метода случайного поиска экстремума может быть рассчитан на нахождение максимума или минимума. Для нахождения противоположного вида экстремума, например, максимума по алгоритму на минимум, необходимо значения оптимизируемой функции f(x) умножить на (-1). Для аналитического метода, в случае дифференцируемости функции f(x) находим f'(x) = 0. Решение полученного уравнения дает оптимальное значение хо. Затем вычисляем f''(хо). Если f''(хо) > 0, то имеем минимум; и если f''(хо) < 0, то максимум (рисунок 3.1). f(x)
хо x
f '(x)
x
f ''(x)
x
Рисунок 3.1 – Графическая интепретация поиска эстремума дифференцируемой функции
Из приведенной графической интерпретации метода следует, что функция (1) имеет максимум и функция (2) – минимум. Среди численных находят применение следующие методы: дихотомии, золотого сечения, Фибоначчи, шаговые и аппроксимации кривыми. Метод дихотомии (половинного деления) является одним из методов одномерной безусловной оптимизации унимодальной целевой функции. Алгоритм метода основывается на выборе исходного отрезка поиска решения [a, b] и его последующем делении пополам: 1) xc=(b+a)/2; 2) x1 = xc - e/2; x2 = xc + e/2; 3) Если при минимизации f(x1) < f(x2), то b = xс, иначе a = xс. 4) При b - a <= e, xопт = (b + a)/2, где e – точность поиска экстремума. Иначе на п. 1.
69.Оценка точности поиска оптимума случайным поиском Методы случайного поиска основаны на формировании на отрезке поиска случайным образом расчетных точек, вычислении в этих точках значений функции и выборе из них экстремального. Точность определяется числом точек поиска n. Повторение испытаний описывается формулой Бернулли (биноминальным распределением)
где k – число благоприятных случаев; n – общее число испытаний; p – вероятность благоприятного исхода при одном испытании; q – вероятность, противоположная p (q=1-p). Вероятность, что событие наступит n раз
что не наступит ни разу
наступит хотя бы один раз
Если абсолютную точность поиска решения на участке (b - a) обозначить через ε, то вероятность решения при одном испытании p = ε/(b - a). При этом вероятности Р1 получения решения в зависимости от числа испытаний n при различных p приведены в таблице 3.1.
Таблица 3.1 – Оценка точности поиска
Например, если p = ε /(b - a)=0.01, то вероятность получения решения с точностью ε при числе испытаний n = 100 равна 0.634; при n =200 – 0.866; при n = 500 – 0.993; при n = 1000 – 0.99996, т.е. требуется 10 (b - a) /ε испытаний для надежного решения (Р1> 0.9999) с заданной точностью ε. Аналогичная зависимость, как видно из таблицы, имеет место и при других точностях решения. 70-71.Отыскание кратчайших расстояний между пунктами транспортной сети. Метод потенциалов Отыскание кратчайших расстояний между пунктами транспортной сети возможно по методу потенциалов, методу "метлы", динамическому методу, на основе теории графов (метод Флойда) и др. Например, задача отыскания кратчайших расстояний между пунктами транспортной сети методом потенциалов решается по следующему алгоритму: 1) Начальному пункту, от которого требуется определить кратчайшие расстояния, присваивается потенциал vi = 0. 2) Находятся все звенья, для которых начальным пунктам i присвоены потенциалы vi, а конечным пунктам j не присвоены. Если таких звеньев нет, то решение закончено (на п.5), а иначе на следующий п.3. 3) Для найденных звеньев по п.2 рассчитываются значения потенциалов конечных пунктов j по следующей формуле: uj(i) = vi + lij, где uj(i) – потенциал конечного пункта j звена i-j; lij – длина звена i-j. Из всех полученных потенциалов выбирается потенциал с наименьшим значением, т.е. определяется:
где { uj(i) } – множество значений потенциалов конечных пунктов j звеньев i-j, i-м начальным пунктам которых ранее присвоены потенциалы; ur(s) – потенциал конечного пункта r звена s-r, являющийся наименьшим по значению элементом множества { uj(i) }. Потенциал ur(s) присваивается соответствующему конечному пункту (vs = ur(s)), а звено r-s отмечается стрелкой. В случае если несколько значений потенциалов множества {vj(i)} окажутся равными и наименьшими, то необходимо установить, относятся они к одному и тому же пункту или нет. Если наименьшие равные значения потенциалов относятся к различным пунктам (у потенциалов не совпадают цифровые индексы без скобок), эти значения потенциалов присваиваются всем соответствующим конечным пунктам и стрелками отмечаются соответствующие звенья. Если наименьшие равные значения потенциалов относятся к одному и тому же конечному пункту r (у потенциалов совпадают цифровые индексы без скобок), то пункту r присваивается это наименьшее значение потенциала и отмечается стрелкой то звено s-r, которому соответствует потенциал ur(s) с большим удельным весом в его составе длин звеньев с лучшими условиями перемещения. При одинаковых дорожных условиях кратчайшее расстояние в этом случае реализуется по одному (любому) из звеньев s-r. 4) переход на п. 2 5) формируется окончательное решение. Величина потенциалов у вершин показывает кратчайшие расстояния от выбранного начального пункта до каждой вершины, а звенья с входящими друг в друга стрелками образуют кратчайший путь движения от интересующего пункта до исходного. Если два пункта сети соединены таким путем, то кратчайшее расстояние между ними равно разности их потенциалов.
72.Выбор переменной для вывода из базиса при решении задачи линейного программирования симплекс-методом
Основные шаги решения задачи (после представления исходной системы в стандартном виде): 11) формируется первоначальное базисное решение; 12) выражается Z через небазисные переменные; 13) проверяется базисное решение на оптимальность. Если оптимально, то на п.10; 14) проверяется задача на наличие решения. Если решения нет, то выход; 15) выбирается из небазисных переменных та, которая способна при введении ее в базис в большей степени улучшить значение целевой функции, и вводится в базис; 16) определяется базисная переменная, которая выводится из базиса; 17) алгебраически выражается вводимая в базис переменная через переменную, выводимую из базиса и другие небазисные переменные; 18) алгебраически выражаются другие базисные переменные через небазисные; 19) переход на п. 2; 20) определяются значения базисных переменных. Они являются решением задачи. Итерационный процесс (шаги 2–9) повторяются до тех пор, пока не произойдет выход на шаге 3 или 4. Алгоритм реализации отдельных шагов при решении задачи на максимум и ограничениях типа £ следующий: Шаг 1 состоит в назначении базисных переменных по числу ограничений в задаче. Базисные переменные xu выражаются через небазисные xp из равенств, в которые они входят через значимые коэффициенты. При этом небазисные переменные принимаются нулевыми. На первом шаге в качестве базисных принимаются дополнительные переменные, а в качестве небазисных – основные, т.е. xm+1 = b1; xm+2 = b2; ... xM = bn; x1 = 0; x2 = 0; ... xm = 0. Шаг 2 – алгебраически выражается целевая функция Z через небазисные переменные
Шаг 3 – проверяется все ли сp≤0. Если да, то решение оптимально. Шаг 4 – оценка наличия решения. Если при хp, имеющем сp >0, во всех уравнениях apj<0 (j =1, 2,..., n), то решение отсутствует (выход из программы с соответствующим сообщением). Шаг 5 – определяется та небазисная переменная, которую наиболее целесообразно ввести в базис, по максимуму положительного коэффициента в текущем выражении для целевой функции Шаг 6 – определяется одна из базисных переменных для вывода ее из базиса. Для этого во всех j-х равенствах для хs вычисляется отношение свободного члена bj к соответствующему коэффициенту asj (asj >0), т.е. bj/asj. Минимальное из отношений указывает на j-е равенство и соответственно на выводимую переменную из базиса. Шаг 10 – формируется окончательное решение в виде численных значений искомых переменных, которые входят в базис. Вычисляются из последних выражений для них при значениях небазисных переменных, равных нулю. С практической точки зрения определение численных значений базисных переменных, которые являются дополнительными, не требуется. Основные переменные, которые не входят в базис, равны нулю.
73.Оптимизация при наличии ограничений. Метод штрафных функций Задача с ограничениями может быть сведена к задаче без ограничений с помощью штрафных функций. Идея внутренних штрафных функций состоит в преобразовании целевой функции Z = f(X)= min и ограничений j j (X) > 0 ( Zш = f(X) + Pш =min;
где r – положительная малая величина; Pш – дополнительная штрафная функция. Если значения Х близкие или равные ограничению, то происходит резкое изменение (увеличение) функции Zш (образуется "гребень" с крутыми краями). Графическая интерпретация приведена ниже на рисунке 3.18.
2 1 Zш
x Рисунок 3.18 – Графическая интепретация метода штрафных функций: 1 – линия ограничения; 2 – функция Zш при большем значении r; 3 – функция Zш при меньшем значении r
Значения r принимаются малыми, чтобы влияние штрафной функции Pш было меньшим в точке оптимума. При меньших значениях r хуже сходимость, при больших значениях – ниже точность решения. Поэтому r необходимо изменять в ходе оптимизации. Существует метод внешних штрафных функций, когда штрафуется удаление от допускаемой области. 74.Оптимизация при наличии ограничений. Метод Лагранжа В отличие от безусловной оптимизации в данном случае установлены ограничения в виде равенств и (или) неравенств в зависимости от X. В этом случае задача состоит в поиске экстремума функции
при выполнении ограничений вида Oj = j j(X) <= >bj, Аналитическое решение задачи при ограничениях типа равенства и дифференцируемости оптимизируемой функции возможно по методу Лагранжа. Для этого вводятся множители Лагранжа lj и с их применением формируется функция L по выражению:
где j j(X)=0. Оптимальные значения вектора X определяются системой m+n уравнений:
ПРИМЕР. Z = 0.5 (x2 - x1) 2 + (1 - x1)2 = min x1 + x2 = 4 или x1 + x2 - 4 = 0 L = 0.5 (x2 - x1)2 + (1 - x1)2 - l (x1 + x2 - 4) = 0
Решение системы уравнений дает следующее решение: x1 = 1.67; x2 = 2.33 и l = 0.67. Без учета ограничений аналитический метод дает решение в точке x1 = 1.0; x2 = 1.0. Графическое представление полученных решений приведено на рисунке 3.16. В случае, если ограничения имеют вид неравенств, необходимые условия нахождения экстремума (минимума) функции f(X) при ограничениях j j (X) £ bj следующие: ограничения в виде неравенств преобразуются в ограничения в виде равенств путем добавления дополнительных (ослабляющих) переменных
формируется функция L с применением множителей Лагранжа
и система уравнений, решение которой определяет точку оптимума
75.Методы решения задачи одномерной безусловной оптимизации
|

 ) к n потребителям Bj (
) к n потребителям Bj ( ). Такой план должен обеспечивать соблюдение ограничений по наличию и потребностям ресурсов, а также минимальные транспортные издержки. Вместо стоимости при поиске оптимальных решений могут приниматься за основу расстояния поставки, время на движение, условные расстояния и другие показатели. Наиболее часто применяются расстояния перевозки.
). Такой план должен обеспечивать соблюдение ограничений по наличию и потребностям ресурсов, а также минимальные транспортные издержки. Вместо стоимости при поиске оптимальных решений могут приниматься за основу расстояния поставки, время на движение, условные расстояния и другие показатели. Наиболее часто применяются расстояния перевозки. ;
;  1Е20, если звена нет)
1Е20, если звена нет) ;
;  ,i¹j
,i¹j  ;
; 
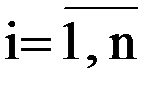 Вывод s i j, p i j pij – промежуточный пункт на пути
Вывод s i j, p i j pij – промежуточный пункт на пути ;
; 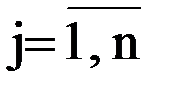 между i и j
между i и j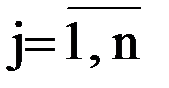 Останов
Останов
 ;
; . Тем самым обеспечивается Xij =0.
. Тем самым обеспечивается Xij =0.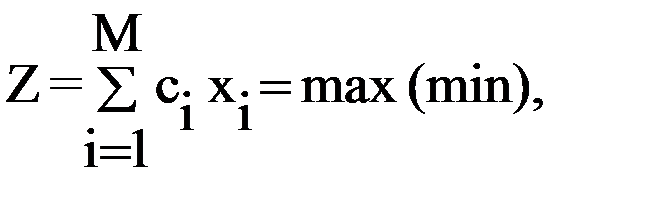
 ;
;
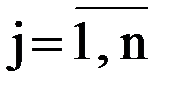
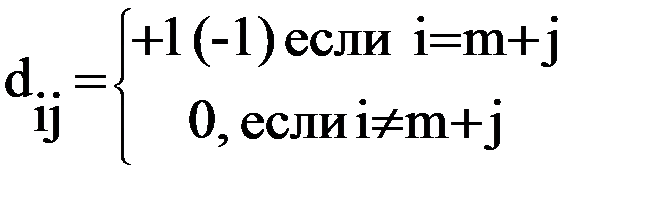 .
. ) к n потребителям Bj (
) к n потребителям Bj (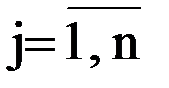 ). Такой план должен обеспечивать соблюдение ограничений по наличию и потребностям ресурсов, а также минимальные транспортные издержки. Вместо стоимости при поиске оптимальных решений могут приниматься за основу расстояния поставки, время на движение, условные расстояния и другие показатели. Наиболее часто применяются расстояния перевозки.
). Такой план должен обеспечивать соблюдение ограничений по наличию и потребностям ресурсов, а также минимальные транспортные издержки. Вместо стоимости при поиске оптимальных решений могут приниматься за основу расстояния поставки, время на движение, условные расстояния и другие показатели. Наиболее часто применяются расстояния перевозки. ; (3.1)
; (3.1)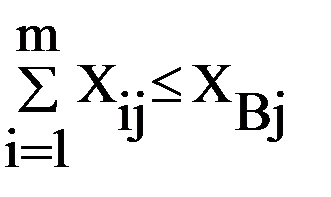 (3.2)
(3.2)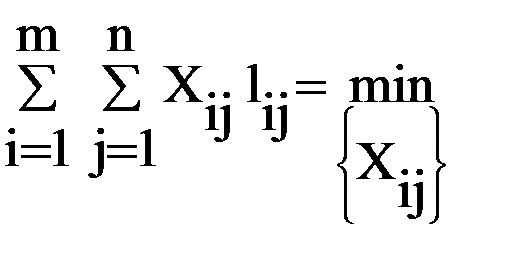 ; (3.3)
; (3.3)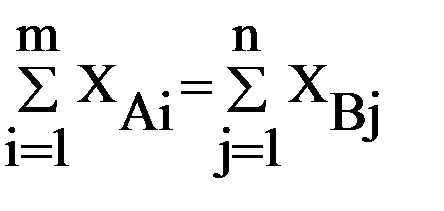 . (3.5)
. (3.5) ;
;  ;
; , k = 0, 1, 2,..., n,
, k = 0, 1, 2,..., n, ;
; ;
;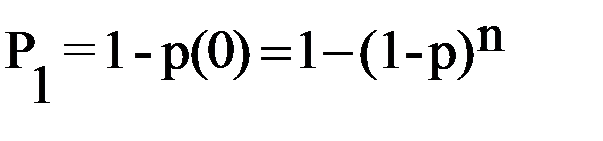 .
. ,
, и
и  . Тогда первое базисное решение
. Тогда первое базисное решение .
. , где s– номер переменной, вводимой в базис.
, где s– номер переменной, вводимой в базис. ) в функцию вида
) в функцию вида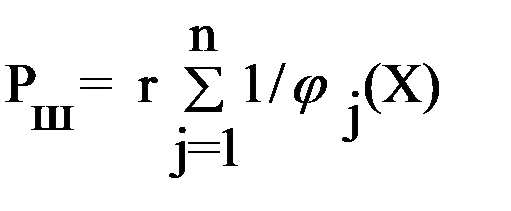 ;
; =min,
=min,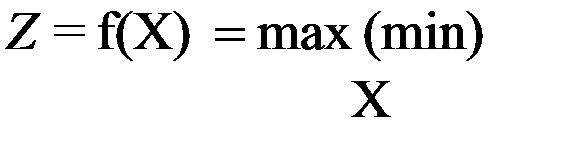 , X = {xi},
, X = {xi}, 
 .
. ,
,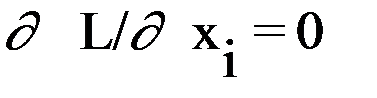 } m – уравнений
} m – уравнений } n – уравнений
} n – уравнений = 0.50 . 2 . (x2 - x1) (-1) + 2 . (1-x1) (-1) - l = 0
= 0.50 . 2 . (x2 - x1) (-1) + 2 . (1-x1) (-1) - l = 0 = 0.50 . 2 . (x2 - x1) - l = 0
= 0.50 . 2 . (x2 - x1) - l = 0 = -(x1 + x2 - 4) = 0
= -(x1 + x2 - 4) = 0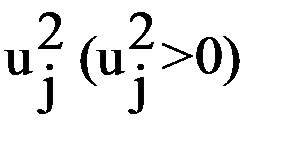 к виду:
к виду: ;
; ;
; } m – уравнений
} m – уравнений } n – уравнений
} n – уравнений } n – уравнений.
} n – уравнений.


