Закон распределения Релея
Функция плотности вероятности
Функция распределения
Точечная оценка параметра закона распределения
Закон распределения Эрланга (гамма-распределение) Функция плотности вероятности
Функция распределения
Точечная оценка параметров закона распределения:
Закон распределения Вейбулла Функция плотности вероятности
функция распределения
Точечная оценка параметров закона распределения
44.Загрузка каналов и их возможные приоритеты в системах массового обслуживания В системах с приоритетами требований различают относительный приоритет (без прерывания обслуживания), когда при поступлении требования с более высоким приоритетом оно принимается на обслуживание после окончания ранее начавшегося обслуживания требования с меньшим приоритетом, и абсолютный приоритет, когда канал освобождается немедленно для обслуживания поступившего требования с более высоким приоритетом. Шкала приоритета может быть построена исходя из каких-то внешних относительно системы обслуживания критериев или на показателях, связанных с работой самой системы обслуживания. Практическое значение имеют следующие типы приоритетов: разделение входящих требований по категориям приоритетности в зависимости от их источников; приоритет у требований с наименьшим временем обслуживания. Эффективность данного приоритета может быть показана на следующем примере. Поступили последовательно два требования с длительностью обслуживания соответственно 6,0 и 1,0 ч. При приеме их на обслуживание освободившимся каналом в порядке поступления простой составит для 1-го требования 6,0 ч и для второго 6,0+1,0 = 7,0 ч или суммарно для двух требований 13,0 ч. Если дать приоритет второму требованию и его принять на обслуживание первым, то его простой составит 1,0 ч и простой другого– 1,0+6,0 = 7,0 ч или суммарно для двух требований 8,0 ч. Выигрыш от назначенного приоритета составит 5,0ч (13-8) сокращения простоев требований в системе; приоритет у требований с минимальным отношением времени обслуживания к мощности (производительности) источника требования, например, к грузоподъемности автомобиля. Механизм обслуживания характеризуется параметрами отдельных каналов обслуживания, пропускной способностью системы в целом и другими данными об обслуживании требований. Пропускная способность системы определяется числом каналов (аппаратов) и производительностью каждого из них. 45.Определение доверительных интервалов случайных величин Интервальная оценка параметра распределения случайной величины определяется тем, что с вероятностью g abs(P – Pм) ≤d, где P – точное (истинное) значение параметра; Pм – оценка параметра по выборке; d – точность (ошибка) оценивания параметра Р. Наиболее часто принимают g от 0.8 до 0.99. Доверительный интервал параметра [Pм–d, Pм+d] – это интервал, в который попадает значение параметра с вероятностью g. Например, на этой основе находится требуемый размер выборки случайной величины, который обеспечивает оценку математического ожидания при точности d с вероятностью g. Вид связи определяется законом распределения случайной величины. Вероятность попадания случайной величины в заданный интервал [Х1, Х2] определяется приращением интегральной функции распределения на рассматриваемом интервале F(Х2)–F(Х1). Исходя из этого, при известной функции распределения можно найти ожидаемое гарантированное минимальное Хгн (x≥ Хгн) или максимальное значение Хгв (x≤ Хгв) случайной величины с заданной вероятностью g (рисунок 2.15). Первое из них является тем значением, больше которого случайная величина будет с вероятностью g, а второе – что случайная величина с вероятностью g меньше этого значения. Гарантированное минимальное значение Хгн с вероятностью g обеспечивается при F(x)= 1-g и максимальное Хгв при F(x)=g. Таким образом, значения Хгн и Хгв находятся по выражениям: Хгн = F-1 (1-g); Хгв = F-1 (g). Пример. Случайная величина имеет экспоненциальное распределение с функцией Требуется найти значения Хгн и Хгв, для которых случайная величина х с вероятностью g=0.95 соответственно больше Хгн и меньше Хгв. Исходя из того, что F-1 (α) = -1/l ln(1- α) (см.вывод ранее) и α = 1-g = 0.05 получаем Хгн = -1/l ln(1- α) = -1/0.01 ln(1-0.05)=-100 (-.0513)=5.13. Для Хгв α = g = 0.95 аналогично имеем Хгв = -1/l ln(1- α) = -1/0.01 ln(1-0.95)=-100 (-2.996)=299.6. Для нормального закона распределения значения Хгн и Хгв могут быть рассчитаны по формулам Хгн = хм + s U1-g = хм - s Ug; Хгв = xм + s Ug,
где xм – математическое ожидание случайной величины; s – среднеквадратическое отклонение случайной величины; Ug – односторонняя квантиль нормального закона распределения при вероятности g.
1.0 F(x) 0.80
0.60 g 0.40
0.20 1-g xгн xгв x
Рисунок 2.15 – Графическая интрепретация определения Хгн и Хгв 46.Описание потоков требований на обслуживание Входящий поток представляет собой последовательность требований (заявок), прибывающих в систему обслуживания, и характеризуется частотой поступления требований в единицу времени (интенсивностью) и законом распределения интенсивности потока. Входящий поток может быть описан также интервалами времени между моментами поступления требований и законом распределения этих интервалов. Требования в потоке могут поступать по одному (ординарные потоки) или группами (неординарные потоки). Свойство ординарности потока заключается в том, что в любой момент времени может поступить только одно требование. Иными словами, свойство заключается в том, что вероятность поступления больше одного требования за малый промежуток времени есть бесконечно малая величина. В случае группового поступления требований задается интенсивность поступления групп требований и закон ее распределения, а также размер групп и закон их распределения. Интенсивность поступления требований может изменяться во времени (нестационарные потоки) или зависит только от единицы времени, принятой для определения интенсивности (стационарные потоки). Поток называется стационарным, если вероятность появления n требований за промежуток времени (t0, t0+Δt) не зависит от t0, а зависит только от Δt. В нестационарном потоке интенсивность изменяется во времени по непериодической или периодической закономерности (например, процессы сезонного характера), а также может иметь периоды, соответствующие частичной или полной задержке потока. В зависимости от того, имеется ли связь между числом требований, поступивших в систему до и после некоторого момента времени, поток бывает с последействием или с отсутствием последействия. Ординарный, стационарный поток требований с отсутствием последействия является простейшим. 47.Критерии согласия Пирсона и Романовского
|

 , x ³ 0;
, x ³ 0; , x ³ 0;
, x ³ 0; .
. , x ³ 0;
, x ³ 0;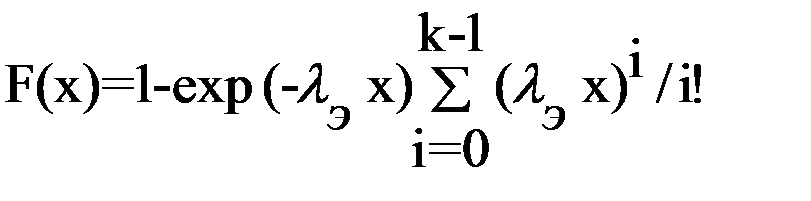 , x ³ 0;
, x ³ 0; и по k' принимается k как ближайшее целое (k=1, 2, 3,...);
и по k' принимается k как ближайшее целое (k=1, 2, 3,...);  .
. , x ³ 0;
, x ³ 0; , x ³ 0;
, x ³ 0; ;
; .
. .
.


