Критерий Сэвиджа
Результаты расчета сожалений по ранее приведенной формуле даны в таблице вторыми строками. Например, для 1-го столбца (Ur=50) сожаления определяются по выражению
По рассчитанным сожалениям поиск оптимального решения проводится следующим образом
Критерий Сэвиджа (критерий минимизации "сожалений") основывается на расчете "сожалений"
К рассчитанным сожалениям применяется решающее правило
Этот критерий минимизирует возможные потери при условии, что состояние среды неблагоприятное. Выбор одного из вышеуказанных критериев в качестве решающего производится принимающим решение. 19.18.Принятие решений в условиях риска Задача в условиях риска состоит в том, что из-за случайности влияния отдельных факторов, например, внешней среды, с каждой принимаемой стратегией Хi связано множество возможных результатов Yj с известными вероятностями p(Yj,Xi), j=1,2,...,J; i=1,2,...,I. При этом достигается эффект V(Yj, Xi). Обобщенной оценкой стратегии Xi является величина ожидаемого эффекта Vo(Xi), рассчитываемая по формуле Если в качестве исходных параметров известны вероятности различных состояний среды, то обобщенная оценка Vo(Xi) стратегии Xi определяется по формуле:
где R – общее число возможных состояний внешней cреды; P(Ur)– вероятность нахождения внешней среды в состоянии Ur (r=1, 2,...,R);V(Xi,Ur) – эффект, который складывается при стратегии Xi и состоянии среды Ur. Принятие решений в условиях риска состоит в определении оптимальной стратегии Xi как
где Vo(Xi) – оценки эффективности (полезности) для стратегий Xi, i =1,2,...,I.
|



 , равных полезности результата
, равных полезности результата  при данном состоянии среды Ur относительно наилучшего решения в зависимости от стратегии Xi, определяемого как
при данном состоянии среды Ur относительно наилучшего решения в зависимости от стратегии Xi, определяемого как 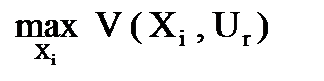 :
: .
. .
. .
. ,
, ,
,


