Законы Зипфа и их применение
Известный американский лингвист и филолог Джордж Зипф (G.K. Zipf) предположил, что слова с большим количеством букв встречаются в тексте реже коротких слов. Основываясь на этом постулате, Джордж Зипф вывел статистические закономерности, которые свойственны всем созданным человеком текстам и не зависят от использованного языка. Обнаруженные закономерности выражаются в одинаковой внутренней структуре текстов и описываются двумя универсальными законами, которые Зипф опубликовал в 1949 году. Первый закон Зипфа «Ранг ‑ частота» Частотой встречаемости слова называется величина, равная числу вхождений слова в текст. Вероятность обнаружения некоторого слова в тексте p равна отношению частоты его вхождения к общему числу слов в тексте. Если все слова одного разговорного языка или просто достаточно длинного текста упорядочить по убыванию частоты их вхождения и пронумеровать, то значение частоты вхождения каждого слова окажется обратно пропорциональным его порядковому номеру. Порядковый номер слова в таком списке является рангом слова и обозначается R. Если несколько разных слов имеют одинаковые частоты, то учитывается только одно из них. Выявленная закономерность описывается первым законом Зипфа: Произведение частоты встречаемости слова на его ранг приблизительно постоянно для любых текстов определенного языка. f R = C, где f ‑ частота встречаемости слова, C — константа Зипфа. Значение константы в разных языках отличается, но внутри одной языковой группы это значение остается неизменным для любого текста. Так, например, для английских текстов константа Зипфа равна приблизительно 1470. Для русского языка эта константа близка к 960.
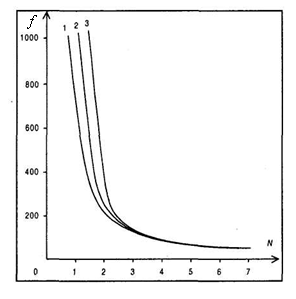
Рис. 1. Кривая зависимости частоты встречаемости слова от его ранга Второй закон Зипфа «количество ‑ частота» В первом законе не учитывался такой факт, что разные слова могут входить в текст с одинаковой частотой. Зипф установил, что частота и количество разных слов N, входящих в текст с данной частотой, также связаны между собой определенной зависимостью. Если построить график, отложив по оси ординат частоту вхождения слова, а по оси абсцисс — количество разных слов, характеризуемых одинаковой частотой, то получившаяся кривая будет сохранять свои параметры для всех без исключения созданных человеком текстов в пределах одного языка. Однако и межъязыковые различия невелики. На каком бы языке текст ни был написан, форма данной кривой Зипфа останется неизменной. Могут незначительно отличаться лишь коэффициенты, отвечающие за наклон кривой. Данное свойство иллюстрируется данными рис. 2., на котором показаны кривые для французского (кривая 1), английского (кривая 2) и русского (кривая 3) языков.
Рис. 2. Полученные Дж. Зипфом результаты могут успешно использоваться на практике для выделения значащих слов в тексте. От того, как будет задан диапазон значимых слов, зависит многое. Если сделать его слишком широким — нужные термины потонут в море вспомогательных слов. Установив же чрезмерно узкий диапазон, мы рискуем потерять некоторые смысловые термины. В каждой поисковой системе данная проблема решается по-своему, руководствуясь общим объёмом текста, специальными словарями и т.п. Интересно отметить, что законы Зипфа весьма универсальны. Они применимы не только к текстам, но и ко многим другим продуктам человеческой деятельности. Например, законам Зипфа соответствуют зависимость количества городов от числа проживающих в них жителей, характеристики популярности узлов в сети Интернет.
|