ПРИЛОЖЕНИЯ. «Современные проблемы социально-гуманитарных наук»

«Современные проблемы социально-гуманитарных наук»

 

КОНТАКТЫ

420015, г. Казань, ул. К. Маркса 51 офис 4,

Научно – образовательный центр «Знание».

Тел.: +7 937 600 79 79. Гумеров Анвар Вазыхович

E-mail: consl@bk.ru.

ВВЕДЕНИЕ

СИСТЕМЫ СЧИСЛЕНИЯ

Понятие о системах счисления. Причины их появления

Позиционные и непозиционные системы счисления

Правила перевода чисел в различные системы счисления

СГЛАЖИВАНИЕ ДАННЫХ СРЕДСТВАМИ

ЭЛЕКТРОННЫХ ТАБЛИЦ

Исходные данные и постановка задачи

Сглаживание на основе встроенных функций

Сглаживание с помощью линий тренда

ЗАКЛЮЧЕНИЕ

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

АЛФАВИТНЫЙ УКАЗАТЕЛЬ

ПРИЛОЖЕНИЯ

 

 

ВВЕДЕНИЕ

В повседневной жизни мы используем десятичную систему счисления, в которой имеется десять базовых цифр от 0 до 9, на основе которых можно построить все остальные числа. Но эта система не является единственной, пример тому – наименования числительных (в давние времена), когда люди считали дюжинами, т.е. использовали 12 различных знаков для записи числа. Одним из главных достоинств этой системы было удобство деления на 2, 3, 4 и 6. Если в русском языке числа 11 и 12 – это 1+10 и 2+10 соответственно, то до сих пор в английском и немецком языках для них существуют специальные слова: 11 – eleven и elf, а 12 – twelve и zwölf. А в древнем Вавилоне астрономы использовали систему счисления с основанием 60, и, по-видимому именно в этом обстоятельстве следует искать объяснение того факта, что час и угловой градус разделены на 60 минут.

 

С математической точки зрения для записи одного и того же числа можно использовать любое (но не меньшее двух) количество символов. Изучение различных систем счисления, которые используются в компьютерах, и арифметических операций над ними очень важно для понимания того, каким образом производится обработка информации в вычислительных машинах.

 

 

1 СИСТЕМЫ СЧИСЛЕНИЯ

1.1 Понятие о системах счисления. Причины их появления

 

Система счисления - совокупность приемов и правил для изображения чисел с помощью символов (цифр), имеющих определенные количественные значения. Системы счисления делятся на непозиционные и позиционные.

 

1.2Позиционные и непозиционные системы счисления

 

Непозиционной системой счисления называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ею позиции (места) в изображении числа, а определяется лишь самим символом (цифрой). Примером такой системы является римская система счисления, в которой: I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000

 

Позиционной системой счисления называется такая система, в которой количественное значение каждой цифры зависит от ее позиции (места) в числе. Любое число в позиционной системе не считая крайних нулей, можно представить единственным образом. Крайняя слева цифра называется цифрой старшего разряда, крайняя справа – цифрой младшего разряда. Позиции каждой цифры в числе присвоен определенный вес d i-1, где i – номер разряда.

 

 

1.3 Правила перевода чисел в различные системы счисления

Для перевода числа из десятичной системы счисления в систему счисления с другим основанием поступают следующим образом:

 

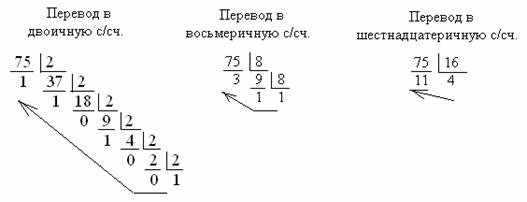
а) Для перевода целой части числа его делят нацело на основание системы, фиксируя остаток. Если неполное частное не равно нулю продолжают делить его нацело. Если равно нулю остатки записываются в обратном порядке.

Таким образом, число 7510 = 10010112 = 1138 = 4В16

 

б) Для перевода дробной части числа ее умножают на основание системы счисления, фиксируя при этом целые части полученных произведений. Целые части в дальнейшем умножении не участвуют. Умножение производиться до получения 0 в дробной части произведения или до заданной точности вычисления.

Таким образом, число 0,9610 = 0,1111012 = 0,753418 = 0.F5C28F16

 

в) Ответ записывают в виде сложения переведенной целой и переведенной дробной части числа.