Минимизация и карты Карно

Поскольку логическую функцию, даже такую простую, как Исключающее ИЛИ, можно реализовать различными способами, часто бывает нужно найти для неё самое простое решение, или, возможно, наиболее удобное схемное решение. Над этой проблемой бились многие светлые умы и в настоящее время существует несколько

способов ее разрешения, включая алгебраические методы, реализуемые с помощью ЭВМ.

При числе входов, не превышающем четырёх, наилучшим методом является составление карты Карно. Этот метод позволяет также найти логи­ческое выражение (если оно заранее неиз­вестно) по таблице истинности. Проил­люстрируем этот метод с помощью при­мера. Предположим, что требуется по­строить схему для мажоритарного под­счета голосов при баллотировке. Будем считать, что имеются три входа, рабо­тающие в положительной логике (на лю­бом из них может быть 1 или 0) и выход (0 или 1). Выход равен 1, если 1 присутствует не менее чем на двух входах.

Шаг 1. Составим таблицу истинности

 

Здесь должны быть представлены все возможные сочетания и соответствующие им состояния выхода (или выходов). В том случае, когда состояние входа не оказывает влияния на выход, ставится X (любое значение).

Шаг 2. Составим карту Карно. Она представляет собой нечто очень близкое к таблице истинности, но содержит пере­менные, которые расположены по двум осям. Переменные должны быть распо­ложены таким образом, чтобы при пере­ходе от каждого квадрата к соседнему менялось бы состояние только одного входа (рис. 6.5).

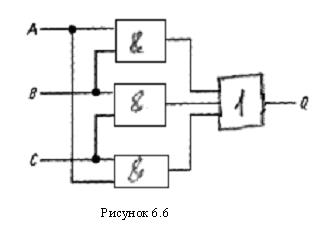
Шаг 3. Отметим на карте группы, со­держащие 1 (можно также использовать и группы, содержащие 0). Три овала на рис. 6.5 определяют логические выраже­ния АВ, АС и ВС.

Далее получим требуемую функцию Q = AB + AC + ВС,

 

 

схемная реализация ее показана на рис 6.6.Этот результат кажется оче­видным, когда он уже получен. Можно было бы составить выражение для нулей и вместо этого получить:

 

 

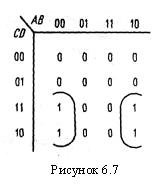
Это выражение может оказаться полез­ным для случая, когда в каких-либо точ­ках схемы имеются дополнения

Некоторые комментарии к картам Карно.

1. Ищите группы, содержащие 2, 4, 8 и т.д. квадратов. Они имеют простые ло­гические выражения.

2. Логика будет тем проще, чем круп­нее блок вы опишете.

3. Состыкуйте края карты Карно. На­пример, карта на рис. 6.7 описывается выражением Q =

4. Блок «единиц», содержащий один или два «нуля», лучше всего описывается с помощью группировки, показанной на рис.6.8. Этому блоку соответствует логическое выражение Q = A ()'.

 

 

5. Места, содержащие X (любое значение),

представляют собой «карт-бланш». Записывайте в них «нули» или «единицы» так, чтобы можно было получить прос­тейшую логику.

6. Карта Карно может и не привести к лучшему решению. Иногда более слож­ное логическое выражение имеет более простую схемную реализацию, например в случае, когда некоторые члены выраже­ния уже сформированы схемой в виде логических

 

 

сигналов, которые можно использовать в качестве входных. Кроме того, реализация функции Исключающее ИЛИ не очевидна из карты Карно. Наконец, при выборе логической структуры схемы определенную роль играют ограничения, связанные с конструкцией ИМС (напри­мер, когда в одном корпусе содержатся четыре 2-входовых вентиля).

Контрольные вопросы

1. Что собой представляет диод Шоттки?

2. Начертите схему 3х–входного ТТЛ вентиля «И–НЕ».

3. Начертите схему 3х–входного КМОП вентиля «ИЛИ».

4. Минимизируйте при помощи карты Карно логическую функцию

Y=X₁X₂X₃ +X₁X₂X₃+X₁X₂ X₃+X₁X₂X_3.
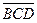