Функция распределения ФермиВероятность того, что при температуре Т энергетический уровень Е занят электроном, определяется функцией распределения Ферми – Дирака. fn (E) = 1 / {exp[(E-Ef) / kT ]+ 1}, где k = 1,38∙10-23 Дж/К – постоянная Больцмана, Еf – уровень Ферми, вероятность нахождения электрона на котором равна 0,5 при Т¹0. Для Т = 0 при Е< Еf f(Е)=1; Е> Еf f(Е)=0; Е=Еf f(Е)=0,5. Т.е. при Т = 0 все уровни выше Еf свободны от электронов, ниже – заняты. Функция имеет ступенчатый характер (рисунок 1.4 – сплошная линия).
Для дырок функция Ферми fp(E) = 1 – fn(E) = 1/{exp[(Ef - E)/ kT ]+ 1}. В собственном полупроводнике уровень Ферми находится посредине запрещённой зоны и распределение электронов в зоне проводимости описывается “хвостом” функции Ферми и, если Е-Еf > 3кТ,единицей в знаменателе можно пренебречь, тогда можно использовать функцию распределения Максвелла – Больцмана. Для электронов fn(E) =exp[–(E-Ef)/ kT ], для дырок fp(E)=exp[– (Ef - E)/ kT. Полупроводник, для которого применимо распределение Максвелла – Больцмана, называется невырожденным. При больших концентрациях примесей уровень Ферми перемещается к границам запрещённой зоны и попадает в валентную зону или зону проводимости. Такие полупроводники называютсявырожденными. Кроме смещения уровня Ферми, в примесном полупроводнике образуются дополнительные локальные уровни. При добавлении донорной примеси образуется донорный уровень ЕД, который располагается под дном зоны проводимости. При Т = 0 К он занят электроном, и при Т > 0 К электроны переходят в зону проводимости (рисунок1.5,а). Так как D ЕД <<; D ЕЗ, то в зону проводимости с донорного уровня переходят больше электронов, чем из валентной зоны.
При воздействии энергии электроны переходят с верхних уровней валентной зоны на свободный акцепторный уровень, и валентная зона становится зоной дырочной проводимости. Mинимальная энергия, которую необходимо сообщить электрону для перехода из валентной зоны на акцепторный уровень, называется энергией ионизации D ЕА акцепторной примеси D ЕА = ЕА – Ев <<; D ЕЗ.
|
При увеличении температуры граница становится расплывчатой. Увеличивается вероятность f(Е) нахождения электронов выше уровня Ферми.
Mинимальная энергия, которую необходимо сообщить электрону для перехода с донорного уровня в зону проводимости, называется энергией ионизации D ЕД донорной примеси D ЕД = ЕС – ЕД.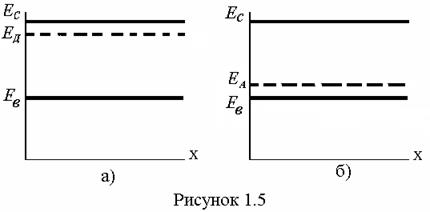
При добавлении акцепторной примеси акцепторный уровень располагается над потолком валентной зоны (рисунок 1.5,б), при температуре абсолютного нуля акцепторный уровень свободен.
