ЛАБОРАТОРНАЯ РАБОТА №2. ЦЕЛЬ РАБОТЫ: изучить законы колебательного движения , определить ускорения силы тяжести.
ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЕ МАТЕМАТИЧЕСКОГО МАЯТНИКА И ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ.
ЦЕЛЬ РАБОТЫ: изучить законы колебательного движения, определить ускорения силы тяжести. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: математический маятник, секундомер, набор шариков, линейка.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Движение, при котором тело или система тел через равные промежутки времени отклоняется от положения равновесия и вновь возвращается к нему, называются периодическими колебаниями. Колебания, при которых изменение колеблющейся величины со временем происходит по закону синуса или косинуса, называются гармоническими. Уравнение гармонического колебания записывается в виде:
Гармонические колебания характеризуются следующими параметрами: амплитудой А, периодом Т, частотой υ, фазой φ, круговой частотой ω. А – амплитуда колебания – это наибольшее смещение от положения равновесия. Амплитуда измеряется в единицах длины (м, см и т. д.). Т – период колебания – это время, в течении которого совершается одно полное колебание. Период измеряется в секундах. υ – Частота колебания – это число колебаний, совершаемых в единицу времени. Измеряется в Герцах. φ – фаза колебания. Фаза определяет положение колеблющейся точки в данный момент времени. В системе СИ фаза измеряется в радианах. ω – круговая частота измеряется рад/с Всякое колебательное движение совершается под действием переменной силы. В случае гармонического колебания эта сила пропорциональна смещения и направлена против смещения:
где К – коэффициент пропорциональности, зависящий от массы тела и круговой частоты.
Примером гармонического колебания может служить колебательной движение математического маятника. Математическим маятником называют материальную точку, подвешенную на невесомой и недеформируемой нити. Небольшой тяжелый шарик, подвешенный на тонкой нити (нерастяжимой), является хорошей моделью математического маятника.
Рис.1 Пусть математический маятник длиной l (рис. 1) отклонен от положения равновесия ОВ на малый угол φ ≤
При малых углах φ можно записать:
где Х – дуговое смещение маятника от положения равновесия. Тогда получим:
Знак минус указывает на то, что сила F направлена против смещения Х. Итак, при малых углах отклонения математический маятник совершает гармонические колебания. Период колебаний математического маятника определяется формулой Гюйгенса:
где Из последней формулы видно, что период колебания математического маятника зависит лишь от длины маятника и ускорения силы тяжести и не зависит от амплитуды колебания и от массы маятника. Зная период колебания математического маятника и его длину, можно определить ускорение силы тяжести по формуле:
Ускорением силы тяжести называется то ускорение, которое приобретает тело под действием силы притяжения его к земле. На основании второго закона Ньютона и закона всемирного тяготения можно записать:
где М – масса Земли, равна R – расстояние до центра Земли, равное Т. к. Земля не имеет форму правильного шара, то на различных широтах имеет разное значение, а, следовательно, и ускорение силы тяжести на разных широтах будет разное: на экваторе
|

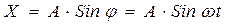
 ,
,
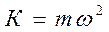
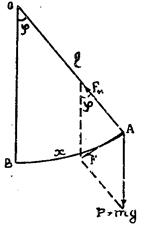
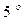 . На шарик действует сила тяжести
. На шарик действует сила тяжести 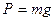 , направленная вертикально вниз, и сила упругости нити
, направленная вертикально вниз, и сила упругости нити 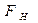 , направленная вдоль нити. Равнодействующая этих сил F будет направлена по касательной к дуге АВ и равна:
, направленная вдоль нити. Равнодействующая этих сил F будет направлена по касательной к дуге АВ и равна:



 - длина маятника, т. е. расстояние от точки подвеса до центра тяжести маятника.
- длина маятника, т. е. расстояние от точки подвеса до центра тяжести маятника.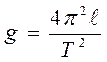
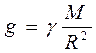
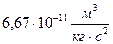
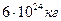 ,
,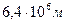 ,
,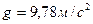 ; на полюсе
; на полюсе 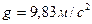 ; на средней широте
; на средней широте  .
.


