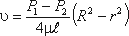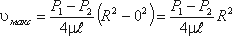Ламинарное течение – упорядоченное течение жидкости, при котором она перемещается как бы слоями, параллельно направлению течения. Скорость в сечении трубы изменяется по параболическому закону (график распределения скоростей по поперечному сечению потока - параболоид вращения): V = V0 (1 – Z2/R2), где R – радиус трубы, Z – расстояние от оси, V0 – осевая (максимальная) скорость течения. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. С увеличением скорости движения ламинарное течение переходит в турбулентное – происходит интенсивное перемещение между слоями жидкости, в потоке возникают многочисленные вихри различных размеров. Профиль осредненной скорости турбулентного течения в трубах отличается от параболического профиля более быстрым возрастанием скорости у стенок и уменьшением кривизной в центральной части течения. За исключением тонкого слоя около стенки, профиль скорости описывается логарифмическим законом. Течение описывается числом Рейнольса: Re = 2RVρ/η, где V – средняя скорость течения, R – радиус трубы, η – коэффициент вязкости. Re критическое = 2300. Re меньше Re критического – ламинарное. Re больше Re критического – турбулентное. Объемная скорость: Q = V/t, где V – объем, t – время через данное сечение. Линейная скорость: V = l/t, l – путь, t – время. Связь линейной и объемной скорости: Q = VS = постоянное (условие неразрывной струи), S – площадь поперечного сечения потока жидкости. Q = (P1 – P2) Пr4/8ηl – уравнение Пуазейля: секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки (градиенту давления в трубе) и четвёртой степени радиуса (диаметра) трубы, только для ламинарного течения: P1 – P2 – падение давления (на входе и выходе), W = 8ηl/ Пr4 – гидравлическое сопротивление сосуда. ∆P = QW, Rаор: Rар: Rкап = 3000: 500: 1. W зависит от радиуса сосуда W = 1/R4, Wкап больше Wар больше Wаор.
Ламинарное течение – упорядоченное течение жидкости, при котором она перемещается как бы слоями, параллельно направлению течения. Скорость в сечении трубы изменяется по параболическому закону (график распределения скоростей по поперечному сечению потока - параболоид вращения): V = V0 (1 – Z2/R2), где R – радиус трубы, Z – расстояние от оси, V0 – осевая (максимальная) скорость течения. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. С увеличением скорости движения ламинарное течение переходит в турбулентное – происходит интенсивное перемещение между слоями жидкости, в потоке возникают многочисленные вихри различных размеров. Профиль осредненной скорости турбулентного течения в трубах отличается от параболического профиля более быстрым возрастанием скорости у стенок и уменьшением кривизной в центральной части течения. За исключением тонкого слоя около стенки, профиль скорости описывается логарифмическим законом. Течение описывается числом Рейнольса: Re = 2RVρ/η, где V – средняя скорость течения, R – радиус трубы, η – коэффициент вязкости. Re критическое = 2300. Re меньше Re критического – ламинарное. Re больше Re критического – турбулентное. Объемная скорость: Q = V/t, где V – объем, t – время через данное сечение. Линейная скорость: V = l/t, l – путь, t – время. Связь линейной и объемной скорости: Q = VS = постоянное (условие неразрывной струи), S – площадь поперечного сечения потока жидкости. Q = (P1 – P2) Пr4/8ηl – уравнение Пуазейля: секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки (градиенту давления в трубе) и четвёртой степени радиуса (диаметра) трубы, только для ламинарного течения: P1 – P2 – падение давления (на входе и выходе), W = 8ηl/ Пr4 – гидравлическое сопротивление сосуда. ∆P = QW, Rаор: Rар: Rкап = 3000: 500: 1. W зависит от радиуса сосуда W = 1/R4, Wкап больше Wар больше Wаор.
Вывод уравнения Пуазейля:
Уравнение, связывающее переменные υ и r, имеет следующий вид:
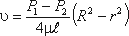
где P1 и P2 - давления в сечениях 1 и 2, μ – динамическая вязкость.
У стенок трубы величина r = R,, значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной
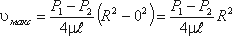
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.
Максимальная скорость дает высоту параболоида

Как известно из геометрии, объем параболоида высотой h и площадью ρR2 равен

а в нашем случае

Закон Пуазейля показывает, что величина Q пропорциональна разнице давления P1 - P2 в начале и конце трубки. Если P1 равняется P2, поток жидкости прекращается. Формула закона Пуазейля также показывает, что высокая вязкость жидкости приводит к снижению объемной скорости течения жидкости. Оно также показывает, что объемная скорость жидкости чрезвычайно зависима от радиуса трубки. Это подразумевает, что умеренные изменения радиуса кровеносных сосудов могут обеспечивать большие различия объемной скорости жидкости, протекающей через сосуд.
Формула закона Пуазейля упрощается и становится более универсальной при введении вспомогательной величины - гидродинамического сопротивления R, которое для цилиндрической трубки может быть определено по формуле:

Закон Пуазейля, таким образом, показывает, что объемная скорость жидкости прямо пропорциональна разнице давления в начале и конце трубки и обратно пропорциональна гидродинамическому сопротивлению:


 Ламинарное течение – упорядоченное течение жидкости, при котором она перемещается как бы слоями, параллельно направлению течения. Скорость в сечении трубы изменяется по параболическому закону (график распределения скоростей по поперечному сечению потока - параболоид вращения): V = V0 (1 – Z2/R2), где R – радиус трубы, Z – расстояние от оси, V0 – осевая (максимальная) скорость течения. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. С увеличением скорости движения ламинарное течение переходит в турбулентное – происходит интенсивное перемещение между слоями жидкости, в потоке возникают многочисленные вихри различных размеров. Профиль осредненной скорости турбулентного течения в трубах отличается от параболического профиля более быстрым возрастанием скорости у стенок и уменьшением кривизной в центральной части течения. За исключением тонкого слоя около стенки, профиль скорости описывается логарифмическим законом. Течение описывается числом Рейнольса: Re = 2RVρ/η, где V – средняя скорость течения, R – радиус трубы, η – коэффициент вязкости. Re критическое = 2300. Re меньше Re критического – ламинарное. Re больше Re критического – турбулентное. Объемная скорость: Q = V/t, где V – объем, t – время через данное сечение. Линейная скорость: V = l/t, l – путь, t – время. Связь линейной и объемной скорости: Q = VS = постоянное (условие неразрывной струи), S – площадь поперечного сечения потока жидкости. Q = (P1 – P2) Пr4/8ηl – уравнение Пуазейля: секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки (градиенту давления в трубе) и четвёртой степени радиуса (диаметра) трубы, только для ламинарного течения: P1 – P2 – падение давления (на входе и выходе), W = 8ηl/ Пr4 – гидравлическое сопротивление сосуда. ∆P = QW, Rаор: Rар: Rкап = 3000: 500: 1. W зависит от радиуса сосуда W = 1/R4, Wкап больше Wар больше Wаор.
Ламинарное течение – упорядоченное течение жидкости, при котором она перемещается как бы слоями, параллельно направлению течения. Скорость в сечении трубы изменяется по параболическому закону (график распределения скоростей по поперечному сечению потока - параболоид вращения): V = V0 (1 – Z2/R2), где R – радиус трубы, Z – расстояние от оси, V0 – осевая (максимальная) скорость течения. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. С увеличением скорости движения ламинарное течение переходит в турбулентное – происходит интенсивное перемещение между слоями жидкости, в потоке возникают многочисленные вихри различных размеров. Профиль осредненной скорости турбулентного течения в трубах отличается от параболического профиля более быстрым возрастанием скорости у стенок и уменьшением кривизной в центральной части течения. За исключением тонкого слоя около стенки, профиль скорости описывается логарифмическим законом. Течение описывается числом Рейнольса: Re = 2RVρ/η, где V – средняя скорость течения, R – радиус трубы, η – коэффициент вязкости. Re критическое = 2300. Re меньше Re критического – ламинарное. Re больше Re критического – турбулентное. Объемная скорость: Q = V/t, где V – объем, t – время через данное сечение. Линейная скорость: V = l/t, l – путь, t – время. Связь линейной и объемной скорости: Q = VS = постоянное (условие неразрывной струи), S – площадь поперечного сечения потока жидкости. Q = (P1 – P2) Пr4/8ηl – уравнение Пуазейля: секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки (градиенту давления в трубе) и четвёртой степени радиуса (диаметра) трубы, только для ламинарного течения: P1 – P2 – падение давления (на входе и выходе), W = 8ηl/ Пr4 – гидравлическое сопротивление сосуда. ∆P = QW, Rаор: Rар: Rкап = 3000: 500: 1. W зависит от радиуса сосуда W = 1/R4, Wкап больше Wар больше Wаор.