Замена переменной – самый общий метод интегрирования
Преобладающим методом интегрирования является метод замены переменной под знаком интеграла или, что то же самое, способ подстановки. Способ подстановки дает возможность интегралы от сложных функций сводить к более простым, а в конечном счете - к табличным интегралам. Для некоторых классов подынтегральных функций можно указать стандартные подстановки, о чем будет сказано в других разделах данного пособия. Начинать же интегрирование способом подстановки лучше всего с простейших интегралов, приводящихся к виду
Иногда удобна подстановка Под знаком дифференциала к независимой переменной всегда можно прибавлять произвольное число (нужное нам), т.к. дифференциал суммы есть сумма дифференциалов, и дифференциал константы равен нулю. Например, для интеграла вида
где После того, как интеграл по новой переменной будет вычислен (взят), в ответе надо перейти к старой переменной, т.е. в полученном решении сделать подстановку Рассмотрим несколько примеров: 9.
10.
11.
12.
13.
14.
15. В следующем интеграле легко заметить, что
16.
Здесь мы выделяем в знаменателе подынтегральной функции полный квадрат и используем постановку
17.
18.
Приведенные выше интегралы могут быть вычислены как формальной подстановкой, так и с помощью подведения под знак дифференциала некоторого множителя подынтегральной функции. Для того, чтобы видеть какую подстановку нужно сделать, следует убедиться, что в подынтегральном выражении можно выделить дифференциал новой переменной. Например, в интеграле
19.
20.
В этом разделе мы рассмотрели простейшие подстановки. В более трудных случаях, чем рассмотреные выше, выбор подстановки не столь очевиден. Однако для некоторых классов подынтегральных функций существуют стандартные подстановки. Об этом мы поговорим ниже, в других разделах.
|

 , где
, где . Подстановкой
. Подстановкой 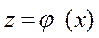 интеграл сведётся к интегралу
интеграл сведётся к интегралу 
 .
. .
. можно под знаком дифференциала умножить и разделить
можно под знаком дифференциала умножить и разделить 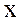 на
на  и прибавить
и прибавить  . Тогда получим:
. Тогда получим:

 .
. (во втором).
(во втором). 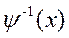 - функция обратная для
- функция обратная для 
 -подстановка
-подстановка




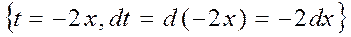








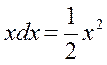 , и поэтому
, и поэтому 


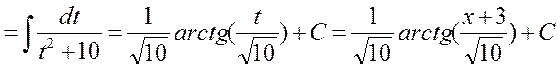
 .
.
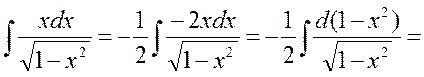
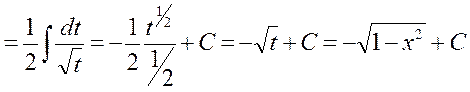

 не рационально делать подстановку
не рационально делать подстановку  , так как
, так как 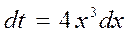 . В числителе же подынтегрального выражения мы имеем только
. В числителе же подынтегрального выражения мы имеем только  . Подстановка
. Подстановка 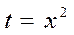 приводит интеграл к табличному.
приводит интеграл к табличному.







