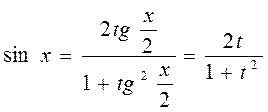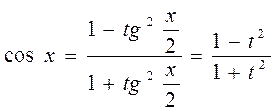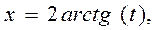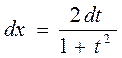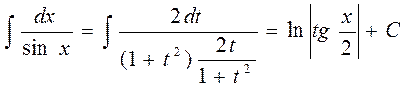Интегрирование выражений, содержащих тригонометрические функции
Рассмотрим несколько типов интегралов от тригонометрических функций: 1. Интеграл вида а) Если хотя бы одно из чисел m или n нечетное и положительное (например, n – нечетное), то рекомендуется подстановка Отделив от Примеры: 36)
37)
б) Пусть теперь m и n четные неотрицательные. В этом случае удобно показатели степеней снизить вдвое, используя известные формулы:
Процесс понижения степеней повторяется до тех пор, пока не получим под знаком интеграла нулевые или нечетные степени 38)
39)
2. Интегралы вида (
Выделяем 2-ю степень Примеры: 40)
Аналогично берется интеграл 41)
3.. Интегралы вида
Можно взять, используя следующие формулы:
Пример: 42)
4.
Эта подстановка может быть использована при интегрировании любой рациональной дроби относительно Примеры: 43)
44) Универсальная подстановка обычно приводит к громоздким выкладкам, поэтому,если есть возможность, пользуются некоторыми частными случаями подстановок. Рассмотрим один такой частный случай.
|

 ,где m и n – целые числа, в некоторых случаях путем простых тригонометрических преобразований можно свести к табличному.
,где m и n – целые числа, в некоторых случаях путем простых тригонометрических преобразований можно свести к табличному.
 (n – нечетное)один множитель
(n – нечетное)один множитель  для получения
для получения  ,оставшуюся четную степень
,оставшуюся четную степень  выражаем через
выражаем через 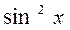 по формуле
по формуле  .
.




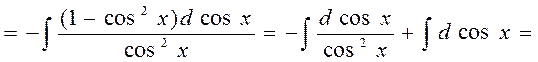




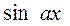 ,
,  .
.



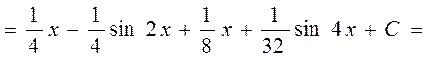






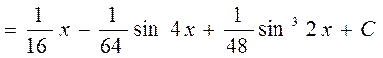
 и
и 
 , целое число) удобно вычислять с помощью следующих подстановок:
, целое число) удобно вычислять с помощью следующих подстановок: и
и 
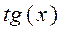 (или
(или  ) и выражаем её через
) и выражаем её через  (или через
(или через  ), постепенно уменьшая степень
), постепенно уменьшая степень  .
.





 ,
, ,
, 





 ,где
,где 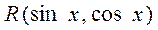 - рациональная дробь относительно
- рациональная дробь относительно  и
и  . Интегралы подобного типа сводятся с помощью универсальной подстановки
. Интегралы подобного типа сводятся с помощью универсальной подстановки  к интегралам от обычной рациональной дроби (относительно
к интегралам от обычной рациональной дроби (относительно  ) (см. стр. 15 - 22). При этом
) (см. стр. 15 - 22). При этом