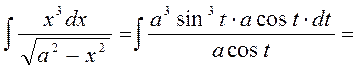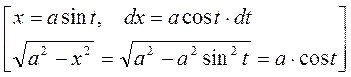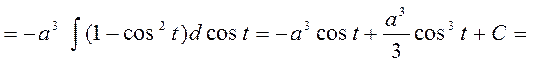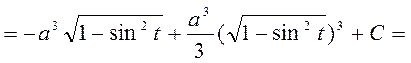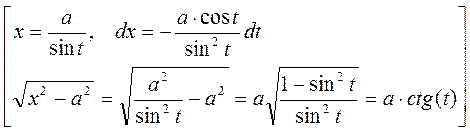Где - функция четная относительно и ,т.е. .В этом случае к более простым вычислениям приводит подстановка .Тогда
45)
Интегрирование рациональных функций, содержащих иррациональности Интегрирование функций, содержащих иррациональности, часто приводит к громоздким вычислениям; кроме того, оно не всегда возможно в конечном виде. Здесь мы рассмотрим только наиболее простые случаи. Подробнее с интегрированием функций, содержащих иррациональности, можно ознакомится в [1],[5] - [8]. Где -рациональная, т.е. содержащая только арифметические действия, функция своих аргументов. Здесь следует сделать подстановку,такую, чтобы корни степени одновременно извлекались (наименьшее общее кратное чисел). Примеры: 46)
47)
2) Для вычисления интеграла вида Пример:
48)
Последний интеграл вычисляется с помощью интегрирования по частям
3) Следующие интегралы берутся с помощью тригонометрических подстановок Для
Вышеуказанные подстановки легко избавляют подынтегральное выражение от иррациональности. Иногда интегралы этих типов могут быть также взяты и при помощи других подстановок. Примеры: 49)
50)
Заключение В пособии рассмотрены основные (простейшие) методы вычисления неопределённых интегралов. Для знакомства с другими методами можно обратиться к рекомендованному списку литературы. Но и в этих книгах нет исчерпывающего набора методов интегрирования. Интегрирование остаётся «искусством» вычисления интегралов.
|
; 
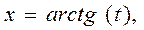
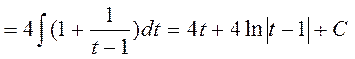
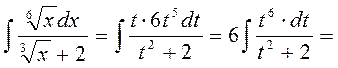
используется подстановка 
.
.
подстановка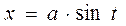 
; для 
подстановка 
.
