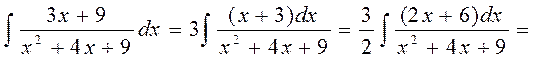Интегрирование по частям. Формулой интегрирования по частям
Формулой интегрирования по частям
имеет смысл пользоваться, когда -- трансцендентных, т.е. показательных, логарифмических, тригонометрических и их попарных произведений; -- произведений трансцендентных и алгебраических функций. Следует помнить, что: 1. d x всегда является частью dV; 2. за U рекомендуется принимать функцию, которая при дифференцировании упрощается и интеграл от которой не является табличным; 3. за dV, как правило, принимаются легко интегрируемые функции; Например, в интегралах типа (k>0, целое число) за U следует принимать В интегралах типа Положить Произвольную постоянную при вычислении V полагаем равной нулю 4. иногда при вычислении исходного интеграла интегрирование по частям приходится применять неоднократно; 5. бывают случаи, когда при интегрировании по частям может оказаться, что
Рассмотрим несколько примеров: 21.
22.
23.
24.
Иногда необходимо провести интегрирование по частям несколько раз. 25.
Повторное применение формулы интегрирования по частям к произведению трансцендентных функций может сводить исходный интеграл к самому себе. 26.
Обозначив исходный интеграл через
Перенося
27.
28.
Интегралы вида Эти интегралы легко вычисляются, если:
знаменателя, т.е.
В первом случае
Здесь при вычислении интегралов использована подстановка
Во втором случае интегралы сводятся к одному из табличных
В общем случае при вычислении указанных интегралов следует: 1. Выделить в числителе производную знаменателя или подкоренного выражения; 2. разбить интеграл на сумму двух, оставляя в числителе подынтегрального выражения первого интеграла выделенную производную; 3. выделить полный квадрат в знаменателе второго интеграла; 4. первый интеграл можно взять используя формулы (1) или (2); второй – одну из формул (3) - (6). Рассмотрим несколько примеров:
29.
30.
|


 проще чем исходный интеграл
проще чем исходный интеграл  . Наиболее целесообразно интегрирование по частям применять при интегрировании следующих функций:
. Наиболее целесообразно интегрирование по частям применять при интегрировании следующих функций:
 .
. нужно
нужно или
или 
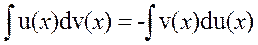 . В этом случае
. В этом случае .
.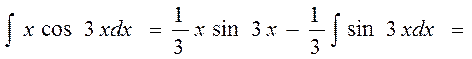


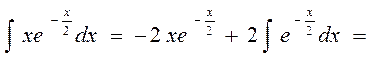







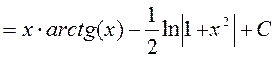

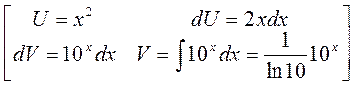




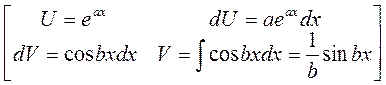


 получим
получим
 в левую часть уравнения, приведя подобные члены и разделив на коэффициент при
в левую часть уравнения, приведя подобные члены и разделив на коэффициент при  ,получим
,получим



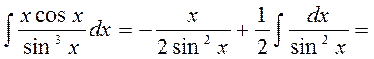



 ;
;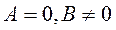 .
.  (1)
(1) (2)
(2)
 (3)
(3) (4)
(4) (5)
(5) (6)
(6)