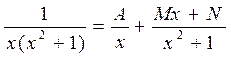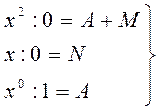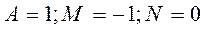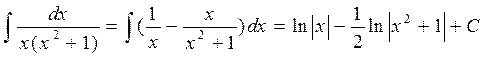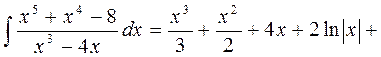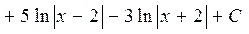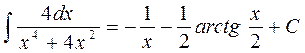Интегрирование рациональных дробей путем разложения их на сумму простейших дробей
Рациональной дробью называется дробь вида m < n, то дробь называется правильной. Во всех остальных случаях – неправильной. Раскладывать на простейшие слагаемые можно только правильные дроби. Если дробь неправильная, то надо разделить числитель на знаменатель с остатком, и этот остаток раскладывать на сумму простейших дробей (для «целой части» получится сумма степенных функций). Т.к. знаменатель есть полином n-й степени, то он имеет ровно n корней, среди которых могут быть вещественные (различные и кратные) и комплексно-сопряженные (различные и кратные). В первом случае полином Поэтому знаменатель Представим правильную рациональную дробь в виде суммы простейших дробей нижеследующего вида:
Далее следует определить коэффициенты в числителях вышеуказанных разложений. Для этого приравняем Другой метод определения коэффициентов Если знаменатель раскладываемой дроби имеет как вещественные, так и мнимые корни, то эти способы можно комбинировать. После вычисления значений коэффициентов Рассмотрим несколько примеров: 31. 1) Дробь неправильная. Выделим целую часть. Для этого разделим числитель на знаменатель. __
__
Таким образом
2) Разложим на множители знаменатель дроби
Корни знаменателя вещественные, разные. 3) Разложим выделенную правильную дробь на простейшие
4) Для определения коэффициентов A, B,C, приравняем числители двух равных дробей (рассматриваемой правильной дроби и суммы простейших дробей после приведения её к общему знаменателю)
Вычислить коэффициенты A, B,C, здесь удобнее методом частных значений. Полагая в последнем выражении последовательно
Окончательно получаем
32) Это дробь правильная. Корни знаменателя вещественные, среди них есть кратные (
Приводим сумму простейших дробей к общему знаменателю и приравниваем числители получившихся дробей
Коэффициенты
Итак
33) Здесь знаменатель подынтегральной функции имеет комплексные корни. Напомним, что каждому неповторяющемуся квадратичному множителю вида
Аналогично получаем 34)
35) Более подробную информацию об интегрировании простейших дробей можно получить в книгах [1], [6], [7] и [8].
|

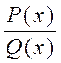 ,где
,где 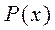 и
и 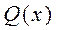 полиномы степеней m и n –соответственно. Если
полиномы степеней m и n –соответственно. Если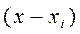 (для каждого из простых корней ) или на
(для каждого из простых корней ) или на 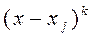 (для каждого из кратных корней; k - кратность корня). Во втором случае полином
(для каждого из кратных корней; k - кратность корня). Во втором случае полином 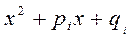 (для простой пары комплексно- сопряженных корней) или на
(для простой пары комплексно- сопряженных корней) или на 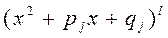 (для каждой кратной пары комплексно сопряженных корней; l - их кратность).
(для каждой кратной пары комплексно сопряженных корней; l - их кратность). - для каждого из простых вещественных корней;
- для каждого из простых вещественных корней;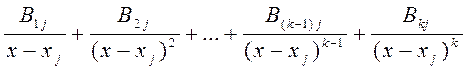 - для каждого из кратных вещественных корней;
- для каждого из кратных вещественных корней; - для каждой из простых пар комплексно-сопряженных корней;
- для каждой из простых пар комплексно-сопряженных корней;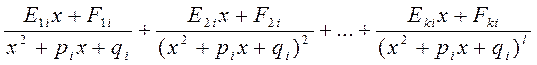 - для каждой из кратных пар комплексно-сопряженных корней.
- для каждой из кратных пар комплексно-сопряженных корней.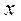 , должны быть равны коэффициенты при одинаковых степенях
, должны быть равны коэффициенты при одинаковых степенях 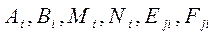 . Вышеописанный метод носит название Метод неопределенных коэффициентов.
. Вышеописанный метод носит название Метод неопределенных коэффициентов.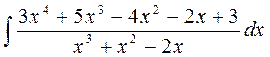
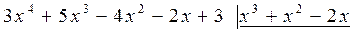
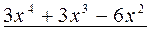
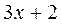
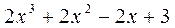
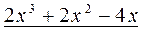


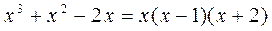


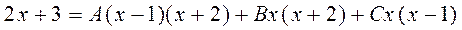
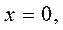

 ,получим
,получим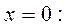
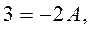
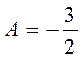




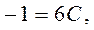
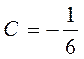

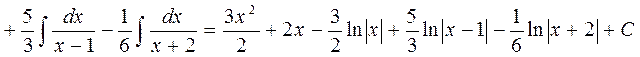
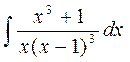
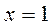 ). Поэтому
). Поэтому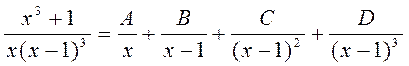
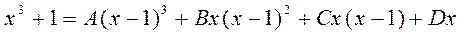
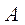 и
и 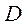 найдем методом частных значений, используя вещественные корни знаменателя
найдем методом частных значений, используя вещественные корни знаменателя 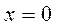 и
и 
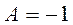
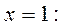


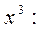
 ,
, 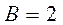
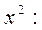

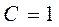
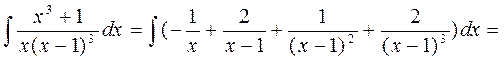
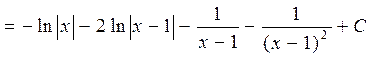

 ,содержащемуся в знаменателе будет соответствовать простейшая дробь вида
,содержащемуся в знаменателе будет соответствовать простейшая дробь вида  . То есть:
. То есть: