Правила интегрирования
Допускается представлять в качестве издательского текстового оригинала четкие распечатки цифрового и текстового материала. 4.4.1. Отпечатки цифр и знаков должны иметь равномерную насыщенность, визуально резкие края и выполняться на бумаге, оптическая плотность которой не более 0,15. Оптическая плотность знаков и цифр должна быть не менее 1,5. 4.4.2. В случае использования распечаток в качестве иллюстраций (образцы программ и т.п.) необходимо при репродуцировании использовать высококонтрастные фототехнические пленки с подбором режима репродуцирования. При необходимости уменьшения размера оригинала-распечатки размер шрифта (цифр и знаков) после репродуцирования должен быть не менее 8 пунктов. 4.4.3. В том случае, если основной объем издания состоит из распечаток с АЦПУ, необходимо изготавливать репродуцируемый оригинал-макет с соблюдением требований п. 4.6.5—4.6.14 настоящего стандарта.
4.5. Издательский текстовой кодированный оригинал) (4.6. Издательский текстовой репродуцируемый оригинал-макет) (4.7. Машинописные оригиналы для листовой и бланочной продукции (для печати на ротапринте) (4.8. Издательский текстовой рукописный оригинал) 4.9. Требования к выходным сведениям
В издательских текстовых оригиналах выходные сведения должны соответствовать требованиям ГОСТ 7.4. Государственное образовательное учреждение Высшего профессионального образования ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» _____________________________________________________________________
В.Б.ОРЛОВ, М.В.ОРЛОВ, И.А.САВУШКИНА
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Учебное пособие
САНКТ-ПЕТЕРБУРГ В.Б. Орлов, М.В.Орлов Неопределённый интеграл: Учебное пособие. - СПБ.; ПГУПС. - 2010. 00 с. Данное учебное пособие предназначено для студентов 1-го курса, начинающих изучать интегральное исчисление. Пособие не содержит теоретических сведений, поэтому при их использовании необходимо наличие лекций или учебника. Рецензенты:
Рассмотрено и одобрено на заседании кафедры «Математика и моделирование», протокол № от 2010 года.
Общие указания Учебное пособие имеет своим назначением помочь студенту в овладении навыками интегрирования. В пособии содержатся рекомендации к вычислению интегралов из широко распространённых сборников задач Б.П.Демидовича и С.Н.Бермана [2], [3]. Пособие не содержит теоретических сведений, поэтому при пользовании им необходимо использование лекций или учебника (использовать можно любой учебник по Высшей математике для ВУЗов и ВТУЗов (Технических университетов)). Например, широко известную книгу Н.С.Пискунова [1]. Очень полезно пособие [8]. Предполагается, что студент обладает твердыми навыками дифференцирования. Методы интегрирования систематизированы по разделам. Настоятельно напоминаем студенту, что как таблицу производных, так и таблицу основных интегралов надо знать наизусть. Это облегчит работу и сэкономит время. В конце учебного пособия приведены варианты контрольных работ. Основные понятия Интегрирование – операция, обратная дифференцированию. Вычислить неопределённый интеграл от некоторой функции f(x)
Операция интегрирования записывается так:
f(x) – называется подынтегральной функцией; f(x)d x – подынтегральное выражение; F(x) – называется первообразной функцией для f(x). Первообразная функция определяется с точностью до произвольной постоянной С. То есть:
Правила интегрирования
Функций
интеграла:
3. Если известна первообразная
4. Интегрирование по частям:
|

 – значит найти функцию F(x), производная от которой равна f(x).
– значит найти функцию F(x), производная от которой равна f(x). (x) = f(x)
(x) = f(x)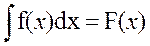
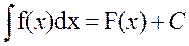
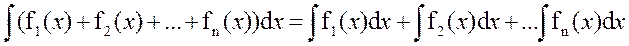
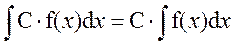
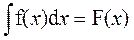 , и x =g(t), то
, и x =g(t), то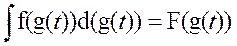 +C
+C



