Набор геометрических операторов проблемно-ориентированного языка ДСАП1
| Наименование операторов
| Описание формата
| Комментарии
| | Задание точки
| I5:N, X, Y
| N — номер точки; Х, Y — координаты точки
| | Задание прямой, проходящей через точки Р/ под заданным углом А к оси ОХ
| 00: N, A, P1, D
| A — угол, град; P1 — -точка 1; D — расстояние
| | Задание прямой, проходящей через две точки
| 01: N, P1, P2, D
| P1 — точка 1; P2— точка 2; D — расстояние
| Задание прямой, параллельной
данной (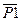 )и отстоящей от нее на расстоянии D )и отстоящей от нее на расстоянии D
| 02: 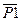 , D , D
| 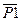 — прямая; D — расстояние — прямая; D — расстояние
| Задание точки как вершины прямоугольника, построенного на заданной прямой 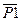
| 03: N,P1,P2, Dl. D2
| Dl>0 — точка справа от Р2; D1<0 — точка слева от Р2 (аналогично для D2)
| | Задание точки, лежащей на прямой, по
одной известной координате
| 04: N, 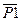 , Z, W , Z, W
| 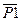 — прямая при X=Z, W=l; Y=Z, W=2 — прямая при X=Z, W=l; Y=Z, W=2
| | Задание точки пересечением двух прямых
| 05: N, 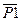 , ,  , Dl, D2 , Dl, D2
| 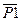 — прямая 1, — прямая 1,  — прямая 2; Dl, D2 — расстояния — прямая 2; Dl, D2 — расстояния
| | Задание точки на окружности по одной известной координате
| 06: N. P1, R, L,W
| D = 1 — точка 1 «входa»; D = 2 — точка 2 «выхода»; X=Z; W=1; Y=Z; W=2; PI— 1центр окружности; R— радиус
| Задание точки пересечения прямой (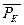 ) с окружностью (Pi, K) ) с окружностью (Pi, K)
| 07: N, P1, R,  W W
|  —прямая; P1—1 центр окружности; R—радиус; W=1 — точка 1 «входа»; W=2 — точка 2 «выхода» —прямая; P1—1 центр окружности; R—радиус; W=1 — точка 1 «входа»; W=2 — точка 2 «выхода»
| | Задание точки пересечения двух окружностей
| 08: R1, P1, Р2, R2, W
| W=1 —точка справа; W=—1 —точка слева
| Определение точки касания прямой (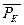 ) и окружности с центром Р ) и окружности с центром Р
| 09: W, P2, 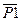
| P1—прямая; Р2—центр окружности; PN—результат
| Определение точки касания прямой, проходящей через заданную точку (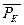 ) к заданной окружности (Pi, R) ) к заданной окружности (Pi, R)
| 10: N, P2, R2, P1, \V
| R—радиус; Р1 — точка; Р2, R2— центр и радиус окружности; W=1—точка;W=—1— точка слева
| | Определение точки касания прямой к двум окружностям (Pi, Rc) и (Рk, Rk)
| 11: N, P1, R1, P2, Wl, W2
| Результат: две точки PN и R(N+1); W1=±1, W2=±l
| | Наименование операторов
| Описание
формата
| Комментарии
| | Задание точки касания двух окружностей
| 12: N, P1, P2, R2
| Р2, R2 — окружность большого радиуса для случая «внутреннего касания»
| | Определение центра окружности (R3), сопрягающей две заданные окружности (Рi, R1) и (Рк, R2)
| 13:N, P1, R1, Р2, R2, W1, W2, Р3
| Wl=l, W2=,l—внешнее касание; W1=—l, W2=—l— внутреннее касание; Р3>0—центр справа; Р3<0—центр слева
| | Определение расстояния между двумя точками (Pi, Рк)
| 14: Р1, P2.D
| Результат: D—расстояние от Р1 до Р2
| | Определение расстояния от точки (X, Y) до прямой Pi
| 15: P1, X, Y, D
| Результат: D — расстояние от точки (X, Y) до прямой Р1
| | Задание точки приращения (∆Х, ∆У) до прямой Р
| 16: N, P1, DX, DY
| Р1— точка; DX, DY — приращения от X и Y
| | Задание точки симметричной данной (Рi) относительно одной из осей координат
| 17: N, P1, W
| PI—точка; W=1—симметрия по оси ОХ, W=2—симметрия по оси OY
| | Определенности центра окружности, проходящей через три точки
| 18: N, P1, P2, РЗ
| PI, P2, РЗ—точки
| | Пересчет координат точек, заданных в локальной системе координат
| 19: I, К, А, X, Y, F
| 1 — начальная точка; К — конечная точка; F=l— правая система; F=1—левая система; А—угол поворота
| | Присвоение
| 20: N, I, К
|
|
Набор геометрических операторов приводится в таблице 6.3.
При помощи операторов, обслуживающих системы, можно получать дополнительную информацию для расчета траектории инструмента.
Для графического контроля результатов расчета на экране дисплея предназначен оператор 14: ЧЕРТЕЖ, позволяющий на любом этапе расчета вывести изображение кодируемого контура детали и сопоставить его с изображением на чертеже. Формат оператора:
<ПАРАМЕТР> — 14: ЧЕРТЕЖ
<ПАРАМЕТР>
<ПАРАМЕТР>
Убедившись, что траектория рассчитана верно, распечатаем координаты опорных точек с выводом информации на экран дисплея. Для этого выполним оператор:
31: 1,9П

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Основные разделы работы участкового врача-педиатра Ведущей фигурой в организации внебольничной помощи детям является участковый врач-педиатр детской городской поликлиники...
Ученые, внесшие большой вклад в развитие науки биологии Краткая история развития биологии. Чарльз Дарвин (1809 -1882)- основной труд « О происхождении видов путем естественного отбора или Сохранение благоприятствующих пород в борьбе за жизнь»...
Этапы трансляции и их характеристика Трансляция (от лат. translatio — перевод) — процесс синтеза белка из аминокислот на матрице информационной (матричной) РНК (иРНК...
|
Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...
Тактика действий нарядов полиции по предупреждению и пресечению правонарушений при проведении массовых мероприятий К особенностям проведения массовых мероприятий и факторам, влияющим на охрану общественного порядка и обеспечение общественной безопасности, можно отнести значительное количество субъектов, принимающих участие в их подготовке и проведении...
Тактические действия нарядов полиции по предупреждению и пресечению групповых нарушений общественного порядка и массовых беспорядков В целях предупреждения разрастания групповых нарушений общественного порядка (далееГНОП) в массовые беспорядки подразделения (наряды) полиции осуществляют следующие мероприятия...
|
|

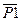 )и отстоящей от нее на расстоянии D
)и отстоящей от нее на расстоянии D
 , Dl, D2
, Dl, D2
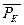 ) с окружностью (Pi, K)
) с окружностью (Pi, K)



