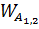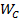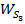Структурный анализ рычажного механизма станка.
2,4-шатуны 3,5-поршни (ползуны) 0-стойка 1.Число подвижных звеньев n=5 2.Число кинематических пар пятого класса Р5=7: 0-1; 1-2; 2-3; 3-0; 1-4; 4-5;5-0. 3.Число кинематических пар четвертого класса Р4=0 4.Степень подвижности механизма-W=1 W=3n-2ps-p4=3·5-2·7-0=1
5.Структурная схема. Разложим механизм на структурные группы Ассура, для чего составим структурную схему. Сначала отсоединим поводковую группу Ассура, состоящий из звеньев 4,5
Рис.3.1.Рычажный механизм строгального станка.
Группа звеньев 4, 5 Группа звеньев 2, 3 Ведущий механизм Структурная схема 2 класс, 2 порядок 2 класс, 2 порядок 1 класс, 1 порядок ,затем группу Ассура, состоящую из звеньев 2,3. Оставшиеся два звена 1,0 образуют ведущий механизм. 6.Класс и порядок каждой группы и ведущего механизма Таким образом, исследуемый механизм, обладающий одной степенью подвижности, может рассматриваться как образованный путём последовательного присоединения к стойке О и ведущему звену двух групп Ассура, состоящих из звеньев 2,3 и 4,5. По классификации И.И.Артоболевского он относится к механизмам 2 класса третьего семейства. 7.Формула строения механизма: I(0-1)->II(2,3)->III(4-5) Кинематическая исследование механизма. 4.1.Исходные данные: Размеры звеньев рычажного механизма, м LOA= LOB= LBC= LCD= y= L1= Частота вращения кривошипа, об/мин n1= Планы механизма. В масштабе µ1= м/мм строим планы механизма, начиная с построения положений ведущего звена – кривошипа ОА. Кривошип изображаем в 8 положениях: через каждые 45˚, начиная с положения, соответствующего своему крайнему левому положению кулисы (ОА0 Планы скоростей. Из полюса Р плана скоростей (рис 4.1.) в направлении вращения кривошипа перпендикулярно к ОA откладываем вектор скоростей Где ω1= Скорость точки А3 кулисы совпадающей с точкой А2 камня, определяется по уравнению (1):
Строим треугольник скоростей точки А согласно уравнению (1), из которого следует
Рис.4.1.Планы скоростей и ускорений Скорость точки С кулисы определяем на основании теоремы о подобии: ω3= Скорость центра масс S3 кулисы 3 определяем на основании теоремы о подобии: ps3=pc3,4∙
Скорость точки Д определяем построением треугольника скоростей согласно уравнению (2):
Значения скоростей точек сведем в таблицу 4.1. Таблица скоростей точек. Таблица 4.1.
Планы ускорений. Из полюса π плана ускорений по направлению от А к О откладываем параллельно ОА вектор Касательное ускорение точки А, WAτ=0, т.к. ω1=const.
Масштаб плана ускорений:
Следующая точка А2 принадлежит камню кулисы. Ускорения точек А1 и А2 будут равны, поскольку размерами камня кулисы пренебрегаем. Точка А2 совершает сложное движение, её ускорение складывается из ускорения точки А3 (переносное движение точки) и ускорения точки А2 при движении звена 2 по звену 3 (относительное движение)
Величину нормального ускорения точки А3 найдем по формуле: Величина ускорения Кориолиса равна: Значение VA3, ω3 и VA2-3, берем из таблицы. Для определения направления ускорения Кориолиса, следует вектор относительной скорости Строим план ускорений точки А2 согласно уравнению а). Далее из конца вектора
Затем из точки начала отрезка К проводим линию действия вектора
Значение величин ускорений определяем из выражений
Величина углового ускорения кулисы ε3 определяем по выражению
Направление ε3 определяется направлением вращения звена 3 вокруг точки В под действием вектора Ускорение точки С находим по выражению:
Ускорение точки D суппорта определяем, построив план скоростей точки Д согласно уравнению
WD∥X-X; Wnдс∥дс WTДС∥дс WD=πd∙µv= м/с2; WTDС=
Значение ускорений точек и углового ускорения кулисы сведём в таблицу 4.2.
Таблица ускорений точек Таблица 4.2.
|

 1-кривошип (коленвал)
1-кривошип (коленвал) 

 = h=
= h= ВА0). Затем изображаем все остальные звенья механизма в положениях соответствующих указанным положениям кривошипа. Положения звеньев на каждом плане механизма определяем методом засечек.
ВА0). Затем изображаем все остальные звенья механизма в положениях соответствующих указанным положениям кривошипа. Положения звеньев на каждом плане механизма определяем методом засечек.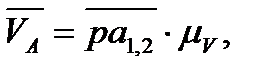 точки А; т.е.
точки А; т.е. 
 ОА. Длиной отрезка ра задаемся ра1,2= мм.
ОА. Длиной отрезка ра задаемся ра1,2= мм. рад/с;
рад/с;  м/с.
м/с. или
или  } (1)
} (1) =pa3∙µV= м/с;
=pa3∙µV= м/с;  =(a3a2)∙µV= м/с.
=(a3a2)∙µV= м/с.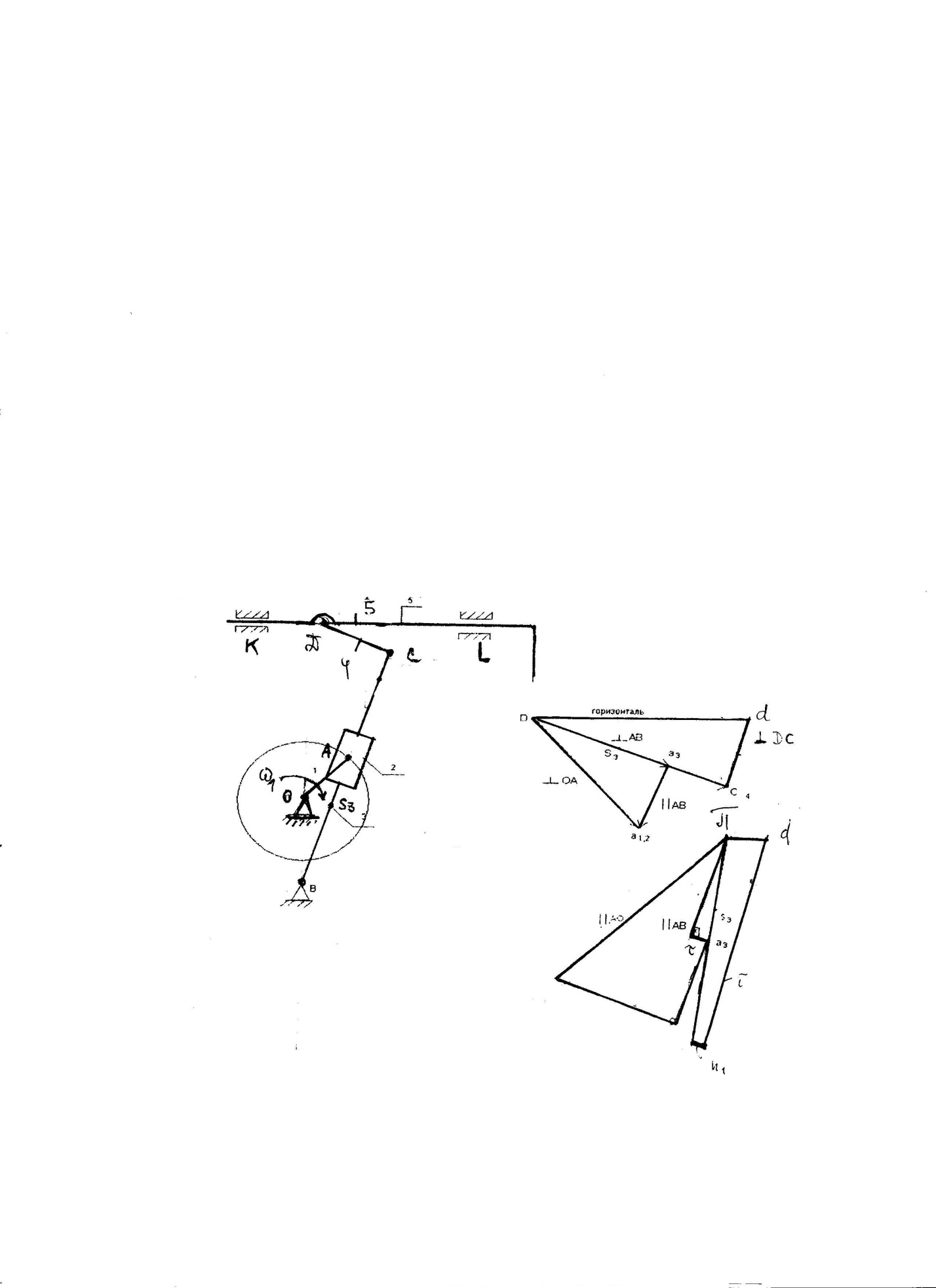
 мм.
мм.  м/с.
м/с. 1/с.
1/с. мм.
мм.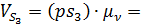 м/с.
м/с. } (2)
} (2)  м/с;
м/с;  .
.  м/с.
м/с.


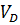


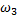

 нормального ускорения точки А кривошипа, который направлен по кривошипу к центру вращения О. Длиной отрезка πа задаемся πа1,2= мм.
нормального ускорения точки А кривошипа, который направлен по кривошипу к центру вращения О. Длиной отрезка πа задаемся πа1,2= мм. = м/с2.
= м/с2.
 ;
; }а)
}а) м/с2.
м/с2.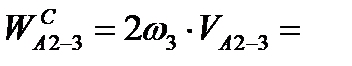 м/с2.
м/с2. повернуть на 90˚ в сторону вращения, обусловленного угловой скоростью ω3.
повернуть на 90˚ в сторону вращения, обусловленного угловой скоростью ω3.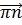 // AB, направленный от точки А к точке В, величина которого равна
// AB, направленный от точки А к точке В, величина которого равна  = мм, а из конца вектора
= мм, а из конца вектора  , который
, который 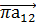 откладываем вектор
откладываем вектор 
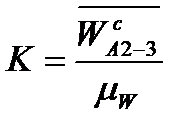 = мм.
= мм. , который // АВ. На пересечении линий получаем точку а3. Соединяя точки π и а3, получим ускорение точки А3-
, который // АВ. На пересечении линий получаем точку а3. Соединяя точки π и а3, получим ускорение точки А3-  .
. = м/с2;
= м/с2;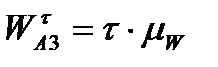 = м/с2;
= м/с2;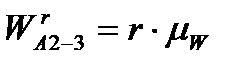 = м/с2.
= м/с2. = м/с2.
= м/с2. = мм;
= мм; = м/с2.
= м/с2.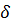 ):
): +WТDC
+WТDC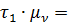 м/с2.
м/с2. =
=  =
=