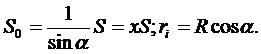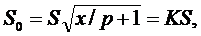Изготовления сферической оболочки

 

Следовательно, заготовка должна иметь плавно изменяющуюся толщину, которую можно вычислить и построить по достаточно большому количеству точек, координируемых углом наклона радиуса и касательной а и проекцией точки касания на диаметр основания полусферы (рис. 268).

При раскатке сферических оболочек неизменной толщины подсчеты сводятся к вычислению для большого количества точек значений.

Для упрощения вычислительных работ значения коэффициента х подсчитаны с высокой точностью при изменении угла α от 0 до 90° с интервалом 10'. В табл. 133 приведены значения х для углов α, взятых с большим интервалом (для 30 точек по радиусу).

 

 

Таблица 133. Значение коэффициента x=1/sin α. Для расчета переменной толщины заготовки при раскатке сферических оболочек

 

Угол α,...°	Значение х	Угол α,...°	Значение х	Угол α,...°	Значение х
	11,408 7,134 5,760 4,810 8,864 3,420 2,921 2,669 2,366 2,203		2,000 1,887 1,174 1,661 1,556 1,491 1,414 1,356 1,305 1,269	85	1,220 1,192 1,155 1,103 1,064 1,035 1,015 1,004 1,0006 1,000

 

На рис. 238 приведен пример расчета и построения заготовки переменной толщины для изготовления сферической оболочки диаметром 1500 мм, толщиной 4 мм. На этом рисунке показано всего лишь несколько сечений, определяемых углами в 15, 30, 45, 60 и 75° (вспомогательная таблица позволяет найти свыше 1000 сечений по диаметру заготовки). Расчетная толщина заготовки для углов, в 30° получается весьма большой и технологически не деформируемой.

В результате плавного изменения толщины заготовки степень обжатия в разных точках заготовки будет различной. Однако не рекомендуется применять обжатие больше 50%. Следовательно, наибольшая толщина должна быть S_o = S\ 0,5 = 8 мм.

Это обжатие соответствует точке окружности, радиус которой наклонен к горизонтали под углом α = 30°.

Для раскатки периферийной части полусферы (с соблюдением правила синусов) необходимо отогнуть фланец обработанной заготовки, как это показано на рис. 238, справа с тем, чтобы этот изгиб давал равновеликие сечения в точках, находящихся между углом 30° и горизонталью, и обеспечивал достаточный объем металла для образования периферийной части полусферы.

Автором предложен метод расчета заготовок для параболических оболочек постоянной толщины. Переменная толщина заготовки параболической оболочки находится по формуле

где р — фокусное расстояние от начала координат (вместо р/2).

Задаваясь различными отношениями х/р (0,01; 0,02; 0,03 и т. д. до 11,0), на счетно-вычислительной машине для 200 точек подсчитаны соответствующие значения коэффициентов кординаты точек параболы могут быть определены теми же параметрами и подсчитаны по формуле

Рис. 239. Способ и пример расчета сечения заготовки