Асимптотическая производительность векторно-конвейерных систем.
Как отмечалось выше, основным признаком векторно-конвейерных систем является наличие конвейерных функциональных устройств, содержащих ряд конвейеров операций (например, конвейер сложения вещественных чисел, конвейер умножения таких же чисел и т.п.). Поэтому оценка производительности векторно-конвейерных систем основана на оценке производительности конвейеров операций. Методику оценки производительности конвейеров операций рассмотрим на примере конвейера операции сложения. Положим, что имеется
где После запуска конвейера и его "разгона" конвейер выдает результат через каждый такт
Быстродействие конвейера Аналогичная ситуация имеет место для конвейеров любых операций. Условно принято говорить, что асимптотическое быстродействие конвейера операций достигается на векторах бесконечной длины. При работе конвейера в последовательном режиме, очевидно, максимальная скорость выдачи результатов равна
Таким образом, конвейерная обработка увеличивает производительность вычислительной системы в
|

 -ступенчатый конвейер операции сложения и пусть все ступени конвейера операций требуют одинакового времени выполнения
-ступенчатый конвейер операции сложения и пусть все ступени конвейера операций требуют одинакового времени выполнения  . Тогда для выполнения операции сложения векторов
. Тогда для выполнения операции сложения векторов  ,
, 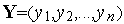 требуется время
требуется время
 - фиксированное время запуска конвейера,
- фиксированное время запуска конвейера,  - время "разгона" конвейера.
- время "разгона" конвейера.
 принято называть асимптотическим быстродействием. Быстродействие конвейера приближается к асимптотическому быстродействию в случае, когда в формуле (1) можно пренебречь слагаемыми
принято называть асимптотическим быстродействием. Быстродействие конвейера приближается к асимптотическому быстродействию в случае, когда в формуле (1) можно пренебречь слагаемыми  много больше величин
много больше величин  . При этом предполагается, что отсутствуют конфликты при обращении к памяти.
. При этом предполагается, что отсутствуют конфликты при обращении к памяти.



