Понятие о внецентренном растяжении и сжатии.
Под нецентренным растяжением и сжатием будем понимать нагружение силами перпендикулярными плоскости поперечных сечений, линия действия которых параллельна продольной оси элемента конструкции, но не совпадает с продольной осью. Нецентренное растяжение и сжатие может иметь место только на массивных конструкциях. При нецентренном растяжении и сжатии элемент конструкции испытывает чистый косой изгиб и осевое растяжение или сжатие.
Порядок расчетов при нецентренном растяжении и сжатии В случаи нецентренного растяжения размеры поперечных сечений известны и требуется определить допустимую нагрузку. Порядок расчетов следующий. При необходимости определяем координаты центра тяжести, положение главных центральных осей инерции и квадранты радиусов инерции, если положение опасных точек не очевидно, определяем положение нейтральной линии и находим координаты опасных точек. Для опасных точек в растянутой и сжатой областях поперечных сечений записываем условие прочности:
Вывод формулы для определения положения нейтральной линии. В формулу
Уравнение нейтральной линии это уравнение прямой не проходящей через начало координат.
|
.
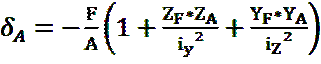=0 подставим координаты точки расположенной на нейтральной линии.
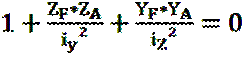уравнение нейтральной линии.
, то 
; 
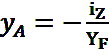- уравнение нейтральной линии в отрезках.
