Определение прогибов при косом изгибе. Понятие об осях большой и малой жесткости

20 Сложное сопротивление. Совместное действие изгибающих моментов и продольной силы.

Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:· косой изгиб;· внецентренное растяжение; изгиб с кручением.При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения. Косой изгиб Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения. Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как сочетание двух плоских изгибов во взаимно перпендикулярных плоскостях. Внецентренным растяжением называется такой вид нагружения бруса, при котором внешние силы действуют вдоль продольной оси бруса, но не совпадают с ней Определение напряжений производится с помощью принципа независимости действия сил. Внецентренное растяжение представляет сочетание осевого растяжения и косого (в частных случаях - плоского) изгиба. Кручение с изгибом Вид нагружения, при котором брус подвергается одновременно действию скручивающих и изгибающих моментов, называется изгибом с кручением.При расчете воспользуемся принципом независимости действия сил. Определим напряжения по отдельности при изгибе и кручении.При изгибе в поперечном сечении возникают нормальные напряжения, достигающие максимального значения в крайних волокнах.

Подобного рода деформация может вызываться или совместным действием на балку продольных и поперечных сил, или только одними продольными силами. Первый случай изображен на Рис.1. На балку АВ действуют равномерно распределенная нагрузка q и продольные сжимающие силы Р.

Предположим, что прогибами балки по сравнению с размерами поперечного сечения можно пренебречь; тогда с достаточной для практики степенью точности можно считать, что и после деформации силы Р будут вызывать лишь осевое сжатие балки. Применяя способ сложения действия сил, мы можем найти нормальное напряжение в любой точке каждого поперечного сечения балки как алгебраическую сумму напряжений, вызванных силами Р и нагрузкой q.

Сжимающие напряжения от сил Р равномерно распределены по площади F поперечного сечения и одинаковы для всех сечений: 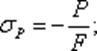нормальные напряжения от изгиба в вертикальной плоскости в сечении с абсциссой х, которая отсчитана, скажем, от левого конца балки, выражаются формулой

Таким образом, полное напряжение в точке с координатой z (считая от нейтральной оси) для этого сечения равно .