


29 Устойчивость сжатых стержней. Вывод формулы Эйлера.
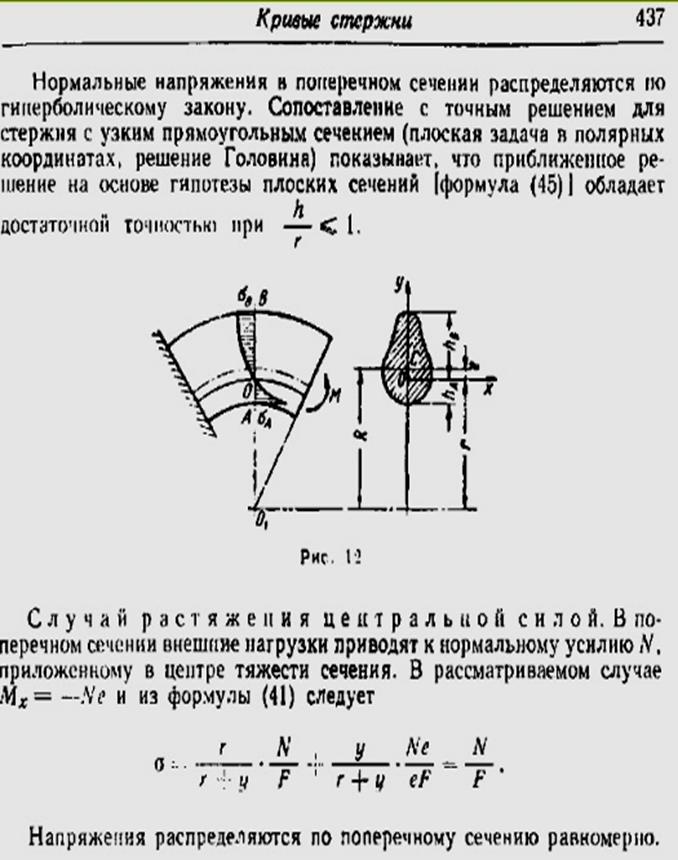
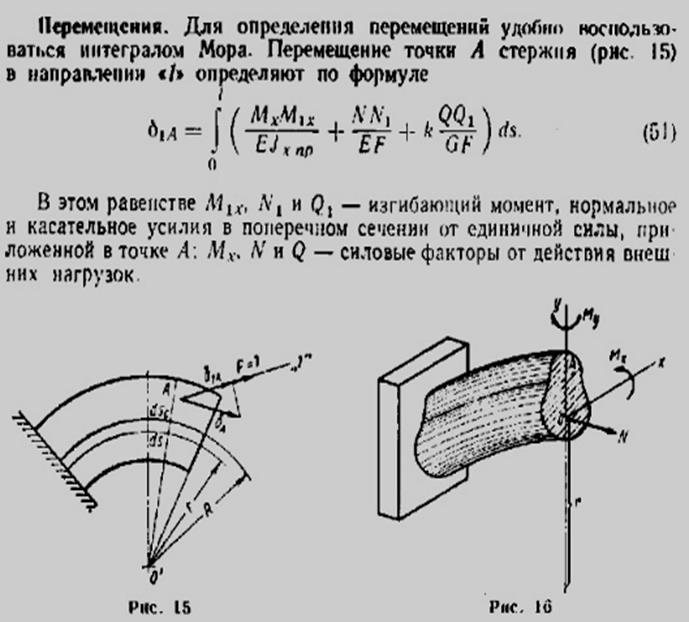
Упругое равновесие устойчиво, если деформированное тело при любом малом отклонении от состояния равновесия стремится вернуться к первоначальному состоянию и возвращается к нему при удалении внешнего воздействия. Нагрузка, превышение которой вызывает потерю устойчивости, называется критической нагрузкой Ркр(критической силой). Допускаема нагрузка [P]=Pкр/ny, ny– нормативный коэффициент запаса устойчивости. Приближенное дифференциальное ур-ние упругой линии:
EJmin=d(*2)y/dx(*2)=M(x), Е –модуль упругости материала стержня, М – изгибающий момент, Jmin– наименьший момент инерции сечения стержня. При потере устойчивости прогиб, как правило, происходит перпендикулярно к оси наименьшей жесткости, относительно которой — J=Jmin. Рассматривается приближенное диффное ур-ие, т.к. потеря устойчивости возникает при малых деформациях. M=-Py, получаем однородное дифф-ное уравнение: (d(*2)y/dx(*2))+k(*2)y=0, где k(*2)=P/EJmin. Решая дифф-ное ур-ие находим наименьшее значение критической силы – формула Эйлера:
Pкр=Пи(*2)EJmin/L(*2) – формула дает значение критической силы для стержня с шарнирно закрепленными концами.
Область применения формулы Эйлера
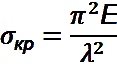
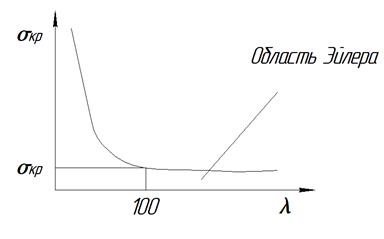
Одним из ограничений принятых Эйлером было принято то, что материал находится в упругом состоянии т.е. критические напряжения не могут превышать предела пропорциональности. Поэтому принимаем равным критическим напряжениям определяем предельную гибкость, гибкость при которой ещё применима формула Эйлера
 Поэтому если действительная гибкость ≥ предельной, то расчёты выполняются по формуле Эйлера.
Поэтому если действительная гибкость ≥ предельной, то расчёты выполняются по формуле Эйлера.
30 Устойчивость сжатых стержней: гибкость стержня, предельная гибкость, формула Ясинского, расчёты на устойчивость.
Гибкость стержня — отношение расчетной длины стержня l0 к наименьшему радиусу инерции i его поперечного сечения. 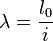 Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба φ. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.Расчетная длина l0 вычисляется по формуле:l0 = μl, где, μ — коэффициент, зависящий от условий закрепления стрежня, а l — геометрическая длина. Расчетная длина, также называется привиденной или свободной.Понятие приведенная длина впервые ввел Ясинский, для обобщения формулы критической силы Эйлера, которую тот выводил для стержня с шарнирно-опертыми концами. Соответственно коэффициент μ равен при шарнирных концах(основной случай) одному, при одном шарнирном, другом защемленным μ = 0.7, при обоих защемленных концах μ = 0,5. Схемы деформирования и коэффициенты μ при различных условиях закрепления и способе приложения нагрузки, изображены на рисунке. Также, стоит отметить, что формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка λ = 100 и выше. При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования.В расчетах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов(длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу. Если гибкость стержня меньше предельного значения
Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба φ. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.Расчетная длина l0 вычисляется по формуле:l0 = μl, где, μ — коэффициент, зависящий от условий закрепления стрежня, а l — геометрическая длина. Расчетная длина, также называется привиденной или свободной.Понятие приведенная длина впервые ввел Ясинский, для обобщения формулы критической силы Эйлера, которую тот выводил для стержня с шарнирно-опертыми концами. Соответственно коэффициент μ равен при шарнирных концах(основной случай) одному, при одном шарнирном, другом защемленным μ = 0.7, при обоих защемленных концах μ = 0,5. Схемы деформирования и коэффициенты μ при различных условиях закрепления и способе приложения нагрузки, изображены на рисунке. Также, стоит отметить, что формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка λ = 100 и выше. При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования.В расчетах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов(длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу. Если гибкость стержня меньше предельного значения 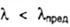 - область ВС на рис. 8.3), то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим. В этих спучаях критическое напряжение определяют по эмпирическим формулам, полученным на основании опытов и приведенных в справочниках. Одна из этих формул - формула Ясинского:
- область ВС на рис. 8.3), то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим. В этих спучаях критическое напряжение определяют по эмпирическим формулам, полученным на основании опытов и приведенных в справочниках. Одна из этих формул - формула Ясинского:  где а, b и с - коэффициенты, зависящие от свойств материала.Для малоуглеродистой стали коэффициенты равны
где а, b и с - коэффициенты, зависящие от свойств материала.Для малоуглеродистой стали коэффициенты равны 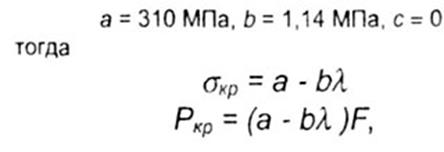 где F - площадь поперечного сечения стержня.
где F - площадь поперечного сечения стержня.
Для коротких стержней, гибкость которых  , расчет на устойчивость не производят. Предельное значение гибкости
, расчет на устойчивость не производят. Предельное значение гибкости 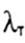 можно найти из условия
можно найти из условия  , где
, где 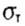 - предел текучести материала стержня.
- предел текучести материала стержня.






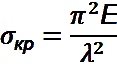

 Поэтому если действительная гибкость ≥ предельной, то расчёты выполняются по формуле Эйлера.
Поэтому если действительная гибкость ≥ предельной, то расчёты выполняются по формуле Эйлера.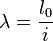 Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба φ. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.Расчетная длина l0 вычисляется по формуле:l0 = μl, где, μ — коэффициент, зависящий от условий закрепления стрежня, а l — геометрическая длина. Расчетная длина, также называется привиденной или свободной.Понятие приведенная длина впервые ввел Ясинский, для обобщения формулы критической силы Эйлера, которую тот выводил для стержня с шарнирно-опертыми концами. Соответственно коэффициент μ равен при шарнирных концах(основной случай) одному, при одном шарнирном, другом защемленным μ = 0.7, при обоих защемленных концах μ = 0,5. Схемы деформирования и коэффициенты μ при различных условиях закрепления и способе приложения нагрузки, изображены на рисунке. Также, стоит отметить, что формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка λ = 100 и выше. При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования.В расчетах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов(длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу. Если гибкость стержня меньше предельного значения
Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба φ. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.Расчетная длина l0 вычисляется по формуле:l0 = μl, где, μ — коэффициент, зависящий от условий закрепления стрежня, а l — геометрическая длина. Расчетная длина, также называется привиденной или свободной.Понятие приведенная длина впервые ввел Ясинский, для обобщения формулы критической силы Эйлера, которую тот выводил для стержня с шарнирно-опертыми концами. Соответственно коэффициент μ равен при шарнирных концах(основной случай) одному, при одном шарнирном, другом защемленным μ = 0.7, при обоих защемленных концах μ = 0,5. Схемы деформирования и коэффициенты μ при различных условиях закрепления и способе приложения нагрузки, изображены на рисунке. Также, стоит отметить, что формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка λ = 100 и выше. При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования.В расчетах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов(длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу. Если гибкость стержня меньше предельного значения 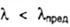 - область ВС на рис. 8.3), то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим. В этих спучаях критическое напряжение определяют по эмпирическим формулам, полученным на основании опытов и приведенных в справочниках. Одна из этих формул - формула Ясинского:
- область ВС на рис. 8.3), то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим. В этих спучаях критическое напряжение определяют по эмпирическим формулам, полученным на основании опытов и приведенных в справочниках. Одна из этих формул - формула Ясинского:  где а, b и с - коэффициенты, зависящие от свойств материала.Для малоуглеродистой стали коэффициенты равны
где а, b и с - коэффициенты, зависящие от свойств материала.Для малоуглеродистой стали коэффициенты равны 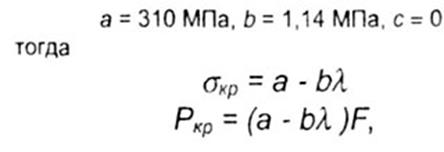 где F - площадь поперечного сечения стержня.
где F - площадь поперечного сечения стержня. , расчет на устойчивость не производят. Предельное значение гибкости
, расчет на устойчивость не производят. Предельное значение гибкости 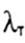 можно найти из условия
можно найти из условия  , где
, где 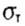 - предел текучести материала стержня.
- предел текучести материала стержня.


