Касательные напряжения при плоском изгибе. (формула Журавского, эпюры)Рассматривая внутренние силовые факторы и напряжения при плоском поперечном изгибе было установлено, что в материале возникают касательные напряжения, по направлению совпадающие с направлением поперечной силы и являющиеся функцией от поперечной силы. При выводе формулы Журавский ввёл ограничения: 1) Материал находится в упругом состоянии и подчиняется закону Гука. 2) Касательные напряжения имеют одинаковую величину в пределах одного слоя и изменяются по высоте поперечного сечения. Рассмотрим как деформируется цельные и составные балки.
Подставляем в уравнение равновесия
Статический момент отсечной площади поперечного сечения относительно нейтрального слоя.
где Q – поперечная сила,
13 Расчет балок на прочность. Балки равного сопротивления изгибу Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко. Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля. Так как изгибающие моменты обычно меняются по длине балки то, подбирая ее сечение по наибольшему изгибающему моменту, мы получаем излишний запас материала во всех сечениях балки, кроме того, которому соответствует Условие, определяющее форму такой балки, имеет вид
Здесь М(х) и W(x) — изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту. Эти условия справедливы и для сечения с наибольшим изгибающим моментом; если обозначить
Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (Рис.1). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.
Рис.1. Расчетная схема балки равного сопротивления
Пусть высота балки будет постоянной По формуле (1) получаем: т. е. ширина меняется по линейному закону в зависимости от х. При Вид балки в фасаде и плане показан на Рис.1. Такое очертание балки получается, если учитывать ее прочность только по отношению к нормальным напряжениям; ширина Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения
Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.
|
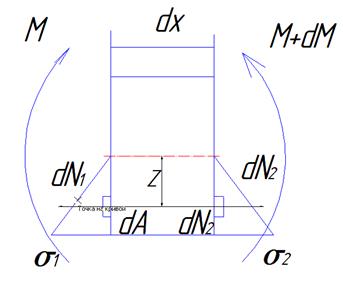Вырежем элементарный объём dx и рассмотрим какие силовые факторы возникают:
; 
; 
;. 
:
- формула Журавского,
- статический момент отсечённой площади поперечного сечения относительно нейтральной оси, 
- осевой момент инерции относительно нейтральной оси, b- ширина слоя, которая определяется касательным напряжением.
12 Проверка прочности по касательным и главным напряжениям при изгибе 
. Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.
и 
— момент сопротивления балки в сечении с наибольшим изгибающим моментом 
, то можно написать:
, а ширина переменной— 
. Момент сопротивления в сечении на расстоянии х от свободного конца будет 
, а изгибающий момент 
; момент сопротивления опорного сечения 
, a наибольший изгибающий момент в опорном сечении 
. В расчете имеют значения лишь абсолютные величины М(х) и 
откуда 
ширина равна 
.
в сечении В обращается в нуль.
или, так как 
