Плоский поперечный изгиб
Плоский поперечный изгиб Под плоским поперечным изгибом понимаем нагружение под действием сосредоточенных и распределённых нагрузок, перпендикулярных к продольной оси, распределённых и сосредоточенных пар сил, если все внешние силовые факторы лежат в одной плоскости, проходящей через продольную ось балки и совпадающей с одной из главных инерционных плоскостей. Элементы, испытывающие нагружение плоского поперечного изгиба будем называть балками. В случае изгиба балки должны опираться на конструкции. Опоры
Для определения внутренних факторов будем использовать метод сечений. В случае плоского поперечного изгиба возникает два силовых фактора: поперечная сила и изгибающий момент. При плоском поперечном изгибе возникают нормальные напряжения, которые являются функциями только изгибающего момента.
При расчёте балок на изгиб необходимо определять законы распределения внутренних усилий по длине балки. Для этого используется метод сечений, строятся эпюры поперечных сил и изгибающих моментов. Дифференциальная зависимость между интенсивностью распределённой нагрузки, поперечной силы и изгибающего момента.
С-центр тяжести поперечного сечения.
С точки зрения геометрии первая производная – тангенс угла наклона касательной, проведённой к графическому изображению поперечной силы (эпюре поперечных сил). Составляем сумму моментов относительно центра тяжести поперечного сечения.
|



 Таким образом при плоском поперечном изгибе в поперечном сечении возникает только нормальные и касательные напряжения.
Таким образом при плоском поперечном изгибе в поперечном сечении возникает только нормальные и касательные напряжения.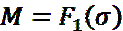 - функция только нормальных напряжений.
- функция только нормальных напряжений. 

 Так как ширина объёма
Так как ширина объёма  мала, то приращение нагрузки за счёт криволинейного характера распределения, является величиной бесконечно малой высшего порядка. Приращением можно пренебречь и принять, что бесконечно малый объём нагружен равномерно-распределённой нагрузкой.
мала, то приращение нагрузки за счёт криволинейного характера распределения, является величиной бесконечно малой высшего порядка. Приращением можно пренебречь и принять, что бесконечно малый объём нагружен равномерно-распределённой нагрузкой. Проецируем все усилия, действующие на элементарный объём, выделенный из балки на вертикальную ось Q+qdx-(Q+dQ)=0; q=
Проецируем все усилия, действующие на элементарный объём, выделенный из балки на вертикальную ось Q+qdx-(Q+dQ)=0; q= 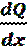 - интенсивность распределенной нагрузки равна первой производной от функции поперечной силы по расстоянию.
- интенсивность распределенной нагрузки равна первой производной от функции поперечной силы по расстоянию.
 .
. ,
,  , при x=0 Q=0, то C=0.
, при x=0 Q=0, то C=0.




