Характер поведения материалов при чистом изгибе. Гипотезы Бернулли.
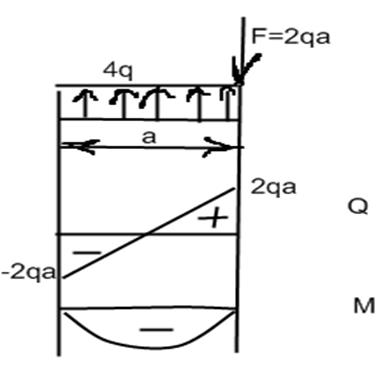
Эпюры Q и М позволяют определить законы распределения внутренних усилий вдоль продольной оси балки и, соответственно, в любом сечениибалки. При плоском поперечном изгибе возникают нормальные и касательные напряжения. Как отмечалось ранее поперечная сила в сечениях складывается из элементарных касательных усилий i FX(Q), а изгибающие моменты - из нормальных усилий, образующих пиры, a = F2(M). Для оценки прочности балок необходимо определить нормальные и касательные напряжения. Если на балке отсутствует поперечная сила, то касательные усилия и напряжения равны нулю и в материале возникают только нормальные напряжения. Изгиб балок, при котором поперечная сила отсутствует (равна 0), называется чистым изгибом. Естественно, что при чистом изгибе в материале возникают только нормальные напряжения. На рис. показаны расчетная схема балки и эпюры Q и M.
Вертикальные линии сетки b - с, d - е - следы поперечны» сечений на боковой поверхности балки, а горизонтальные g - f, т - п следы слоев на боковой поверхности. Нагрузим балку статически и про анализируем поведение сетки. В деформированном состоянии участии балки с сеткой показан на рис. 184.
При нагружении вертикальные линии b - с, d - е, прямолинейные до нагружения, остались прямолинейными в процессе нагружения и повернулись относительно своего первоначального положения на некоторый угол, Горизонтальные линии g —f, т-п при нагружении стали криволинейными и слой g -/испытал деформацию сжатия, а слой т-п- деформацию растяжения, следовательно, существует некоторый слой ООи который не изменяет при нагружении линейные размеры - нейтральный слой. На основании приведенных экспериментальных данных сформулируем гипотезы Бернулли: 1. Гипотеза плоских сечений: поперечные сечения, плоские до нагружения, остаются плоскими в процессе нагружения и поворачиваются на некоторый угол относительно первоначального положения. 2. Продольные слои друг на друга не давят и под действием нормальных напряжений испытывают линейные деформации растяжения и сжатия. 3. Напряжения в пределах одного слоя поперечного сечения постоянны по величине и изменяются по высоте поперечного сечения. Гипотезы Бернулли справедливы, если выполняются следующие ограничения: 1. Материал балок находится в упругом состоянии и подчиняется чакону Гука. 2. Соотношения между размерами поперечных сечений и длиной балки таковы, что не происходит скручивание и коробление. Поперечное сечение имеет хотя бы одну ось симметрии, и все внешние силы лежат в плоскости симметрии балки. 3 Изгиб прямого бруса: основные положения, …
Правило знаков: 1) Изгибающий момент + если внешний момент стремиться повернуть сечение т.о. чтобы сжимать верхние волокна 2) эпюры изгибающих моментов всегда строятся на сжатых волокнах 3) поперечная сила + если внешняя нагрузка стремится повернуть сечение по часовой стрелке Пусть брус нагружен произвольным образом распределенной нагрузкой q = f (z) (рис. 5.5, а).
Рис. 5.5 Выделим из бруса элемент длиной dz и приложим по его краям положительные внутренние усилия (рис. 5.5, б). В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, проходящей через точку С (рис. 5.5, б), получим: Qy + q dz - Qy - d Qy = 0; Mx + Qy dz + q dz × dz /2 - Mx - d Mx = 0. Производя упрощения и отбрасывая величины высшего порядка малости, получим: Из (5.4) следует, что при q = const функция Qy будет линейной, а функция Mx - квадратичной. Если на каких-то участках бруса распределенная нагрузка отсутствует, т.е. q = 0, то получим, что Qy = const, а Mx является линейной функцией от z. В сечениях, где приложена сосредоточенная сила, эпюра Qy претерпевает скачок на величину внешней силы. И наконец, в тех сечениях, где Qy принимает нулевое значение и меняет знак, функция Mx достигает экстремальных значений. Для исследования напряженного состояния тела в любой его точке нужно уметь определять напряжения не только на площадках, параллельных координатным плоскостям, но и на наклонных. Положение бесконечно малой наклонной площадки
Рис.1.2. Напряжения на наклонной площадке Наклонная площадка и координатные плоскости образуют бесконечно малый тетраэдр Рассмотрим силы, действующие на тетраэдр. На координатных площадках это будут силы от шести составляющих напряжений Спроектируем действующие силы на ось х: Опуская слагаемое третьего порядка малости и разделив все на Аналогичным образом можно получить еще два уравнения, и тогда уравнения равновесия элементарного тетраэдра имеют вид
Уравнения (1.4) позволяют выразить напряжения на любой наклонной площадке с нормалью Если наклонная площадка совпадает с поверхностью тела, то составляющие Главные напряжения. Инварианты напряженного состояния При помощи уравнений (1.4) можно вычислить напряжения на любой наклонной площадке в любой точке внутри тела, если известны составляющие напряжения Равнодействующая составляющих напряжения
Нормальное напряжение равно сумме проекций составляющих полного напряжения, параллельных координатным осям, на направление нормали:
Подставляя значения из (1.4), получим
Выражение (1.7) позволяет определять нормальные напряжения на любой наклонной площадке с помощью шести составляющих напряжений на трех площадках, параллельных координатным плоскостям. При этом касательные напряжения на этой площадке будут
Формула (1.8) дает величину касательного напряжения, но не позволяет определить его направление в плоскости площадки. Определим составляющую касательного напряжения в плоскости площадки с нормалью
Искомое касательное напряжение равно сумме проекций составляющих напряжений Подставим в это выражение составляющие напряжения из (1.4):
Выражение (1.10) позволяет определить касательные напряжения на любой наклонной площадке в заданном направлении с помощью шести составляющих напряжений на трех площадках, параллельных координатным плоскостям. Площадка, на которой касательные напряжения равны нулю, называется главной. Для такой площадки ( Из условия Сравнивая эти соотношения с (1.4), получим:
Из аналитической геометрии известно соотношение между направляющими косинусами:
Уравнения (1.11) и (1.12) содержат четыре неизвестных: главное напряжение и три его направляющих косинуса. Преобразуем (1.11) к виду
Эта система имеет ненулевое решение (нулевое решение невозможно в силу (1.11)) тогда и только тогда, когда ее определитель равен нулю: Раскрывая определитель и группируя по степеням
или
где
Решение уравнения (1.14) всегда дает три действительных корня. Наибольший по алгебраическому значению корень обозначается через Подставляя значение одного из главных напряжений в (1.13), можно найти направляющие косинусы Обозначим два главных напряжения через
Умножим уравнения (1.16) на Т.к. Аналогично можно доказать ортогональность главных площадок, на которых действуют другие пары главных напряжений. Таким образом, в каждой точке тела можно выделить по крайней мере три главных площадки, которые взаимно перпендикулярны друг другу. Величины главных напряжений не зависят от положения координатных осей Если их выразить через главные напряжения (а для этого в (1.15) нужно касательные напряжения принять равными нулю), то получим
В теории напряжений инварианты рассматриваются как основные характеристики напряженного состояния тела в данной точке. 5 Изгиб прямого бруса: построение эпюр поперечных сил и изгиб моментов (правила построения и контроля эпюр; эпюры при нагружении однопролетной балки сосредоточ силой; эпюры при нагружении однопролетной балки распредел нагрузкой) 1)сосредоточ сила, прилож на конце консоли дает на эп Q скачек на велич силы, а на эп М наклон линию 2) на участках где прилож равномерно распредел нагрузка, эп Q всегда наклонная линия, а эп М квадратич парабола. Эп М на встречу стрелкам, как зонтик.
1) Сосредоточенная нагрузка на эпюре Q дает скачок на величину нагрузки, а на эпюре М излом.
2) см вопр 5 3) сечение в кот эп Q пересек ось, эп М приним экстремальное значение 0) Определ. реакции опор и считаем число участков 1) строим эпюры поперечных сил и изгибающих моментов и на эпюре изгиб моментов находи опасные моменты. Под опасным понимается сечение в которых изгиб момент принимает макс. Значение, это справедливо для изотропных и анизотропных материалов с симметричным сечением. 2) Производим расчет по формуле
Для анизотропных симметричных материалов в качесвте допуск. Напряжения берется наименьшее. Для нессиметр. Анизотропных материалов надо производить отдельно расчет, как по допускаемым напряжениям сжатия и на разжатие. 8. Центр изгиба: понятие и экспериментальное определение ЦЕНТР ИЗГИБА -точка поперечного сечения бруса, такая, что брус при изгибе не испытывает кручения, если поперечная сила проходит через Ц. и. В упругом брусе положение Ц. и. не зависит от величины силы. Определение Ц. и. важно для расчёта ряда конструкций. Напр., чтобы крыло самолёта в полёте не изменяло самопроизвольно угол атаки, надо профиль крыла выбрать т. о., чтобы подъёмная сила проходила через Ц. и. Что такое ЦЕНТР ИЗГИБА СТЕРЖНЯ? Описание термина. точка в плоскости поперечного сечения тонкостенного стержня, обладающая тем свойством, что проходящие через неё поперечные силы вызывают изгиб стержня без кручения У тонкостенных нессиметрич профилей центр изгиба не совпадает с центром тяжести фигуры при изгибе параллельного плоскости не явл осью симметрии(в то же время явл главной осью симметрии)
9 Понятие о прогибе и угле поворота. Вывод приближённого дифференциального уравнения изогнутой
оси Перемещение центра тяжести поперечного сечения в направлении, перпендикулярном первоначальному положению продольной оси будем называть прогибом. Конечные элементы, перпендикулярные к продольной оси, остаются перпендикулярными упругой оси при нагружении.
Вывод приближённого дифференциального уравнения изогнутой оси
Методика решения следующая: 1.
Проводим сечение с учётом правила знаков построения эпюр записываем уравнение изгибающего момента:
Постоянные интегрирования – это угол поворота и прогиб, выбранные в начале координат. В чисто виде приближённое дифференциальное уравнение изогнутой оси применять для определения прогибов и углов поворота оказывается не всегда возможным. В случае действия многих сил возрастает количество необходимых дифференциальных уравнений и, естественно, возрастает количество постоянных интегрирования, которые определить сложно, так как возникают сложности в назначении граничных условий.
|





 (5.4) откуда
(5.4) откуда 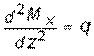 (5.5)
(5.5) (рис.1.2) определяется нормалью
(рис.1.2) определяется нормалью  с направляющими косинусами
с направляющими косинусами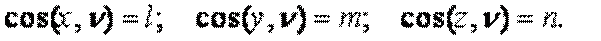

 Обозначим площадь наклонной площадки через
Обозначим площадь наклонной площадки через  и свяжем с ней площади остальных граней тетраэдра:
и свяжем с ней площади остальных граней тетраэдра:
 а на наклонной — силы от трех составляющих полного напряжения
а на наклонной — силы от трех составляющих полного напряжения 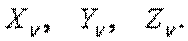 Кроме того, по всему объему тетраэдра действуют составляющие
Кроме того, по всему объему тетраэдра действуют составляющие  объемной силы.
объемной силы.
 получим
получим

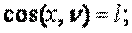
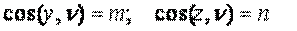 через шесть направляющих напряжений, параллельных координатным плоскостям.
через шесть направляющих напряжений, параллельных координатным плоскостям. полного напряжения соответствуют составляющим внешних сил, действующих на поверхности тела. Тогда уравнения (1.4) будут называться условиями на поверхности тела и свяжут внешние силы с внутренними.
полного напряжения соответствуют составляющим внешних сил, действующих на поверхности тела. Тогда уравнения (1.4) будут называться условиями на поверхности тела и свяжут внешние силы с внутренними.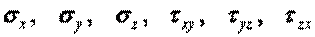 по трем взаимно перпендикулярным площадкам, параллельным координатным плоскостям.
по трем взаимно перпендикулярным площадкам, параллельным координатным плоскостям.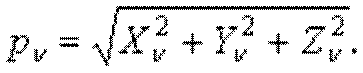


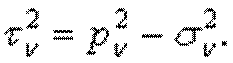
 с направляющими косинусами
с направляющими косинусами  Направления
Направления 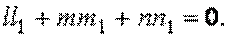


 ) из (1.8) следует
) из (1.8) следует  т.е. на главной площадке полное напряжение совпадает с нормальным как по величине, так и по направлению.
т.е. на главной площадке полное напряжение совпадает с нормальным как по величине, так и по направлению.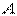 , спроектируем его на координатные оси и найдем составляющие главного напряжения, параллельные координатным осям:
, спроектируем его на координатные оси и найдем составляющие главного напряжения, параллельные координатным осям: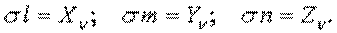







 наименьший —
наименьший — 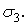 Таким образом
Таким образом
 соответствующей главной площадки.
соответствующей главной площадки. ,
,  , а их направляющим косинусам придадим значения с соответствующими индексами и дважды запишем уравнения (1.13):
, а их направляющим косинусам придадим значения с соответствующими индексами и дважды запишем уравнения (1.13):
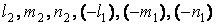 соответственно и сложим их:
соответственно и сложим их:
 то получаем условие ортогональности главных площадок, на которых действуют
то получаем условие ортогональности главных площадок, на которых действуют 
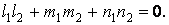
 следовательно, корни кубического уравнения (1.14) не зависят от выбора координатной системы и коэффициенты этого уравнения должны сохранять постоянные значения при преобразовании осей, т.е. они являются инвариантами, поэтому величины
следовательно, корни кубического уравнения (1.14) не зависят от выбора координатной системы и коэффициенты этого уравнения должны сохранять постоянные значения при преобразовании осей, т.е. они являются инвариантами, поэтому величины 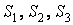 называются соответственно первым, вторым и третьим инвариантами напряженного состояния.
называются соответственно первым, вторым и третьим инвариантами напряженного состояния.

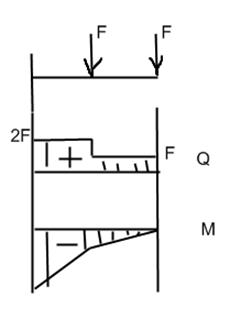

 - угол поворота, т.е. угол, на который поворачивается поперечное сечение балки при нагружении относительно своего начального положения.
- угол поворота, т.е. угол, на который поворачивается поперечное сечение балки при нагружении относительно своего начального положения. 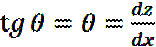 . Угол поворота – это производная прогибов по расстоянию. Величиной прогибов оценивается жёсткость элементов конструкции и величина максимальных прогибов регламентирована. Величина прогиба:
. Угол поворота – это производная прогибов по расстоянию. Величиной прогибов оценивается жёсткость элементов конструкции и величина максимальных прогибов регламентирована. Величина прогиба:  . Величина предельного прогиба, как правило устанавливается в соответствии с техническими условиями на конструкции.
. Величина предельного прогиба, как правило устанавливается в соответствии с техническими условиями на конструкции.  .
.
 ,
, 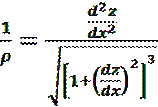 . Пренебрегаем первой производной от прогиба по расстоянию как величиной бесконечно малой по сравнению с единицей и получаем следующее уравнение:
. Пренебрегаем первой производной от прогиба по расстоянию как величиной бесконечно малой по сравнению с единицей и получаем следующее уравнение:  , где M(x)-изгибающий момент,
, где M(x)-изгибающий момент,  -главный момент инерции относительно нейтральной оси.
-главный момент инерции относительно нейтральной оси.




