Если толщина стенок цилиндра 
мала по сравнению с радиусами 
и 
, то известное выражение для тангенцальных напряжений приобретает вид 
Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределенным симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений. Выделим из рассматриваемого резервуара элемент двумя смежными меридиональными сечениями и двумя сечениями, нормальными к меридиану. Размеры элемента по меридиану и по перпендикулярному к нему направлению обозначим соответственно 
и 
, радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим 
и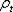 
, толщину стенки назовем t. По симметрии по граням выделенного элемента будут действовать только нормальные напряжения 
в меридиальном направления и 
в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут 
и 
. Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану. Усилия 
дадут в нормальном к поверхности элемента направлении равнодействующую ab, равную 
Подобным же образом усилия 
дадут в том же направлении равнодействующую 
Сумма этих усилий уравновешивает нормальное давление, приложенное к элементу 
Отсюда 
Это основное уравнение, связывающее напряжения и для тонкостенных сосудов вращения, дано Лапласом. Так как мы задались распределением (равномерным) напряжений по толщине стенки, то задача статически определима; второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара.
