Основные и простейшие задачи аналитической геометрии

Скажи: «Достаточный свидетель между мной и вами –

Аллах и тот, кто знает Книгу!»

Основные и простейшие задачи аналитической геометрии

В аналитической геометрии изучаются две основных задачи:

1. Нахождение уравнения геометрического объекта, который рассматривают как геометрическое место точек, которые имеют определенное свойство.

2. Исследования свойств геометрического объекта по его уравнению и построение его.

К простейшим задачам аналитической геометрии относятся такие две:

1) нахождения расстояния между двумя точками;

2) деления отрезка в заданном отношении.

Пусть заданны точки М₁ и М₂ в пространстве, то есть каждая из них имеет три координаты М₁(х₁,у₁,z₁), М₂(х₂,у₂,z₂). Расстояние между точками М₁ и М₂ и равно длине вектора , координаты которого равны разности одноименных координат точки М₂ и точки М₁. Длина вектора равна квадратному корню из суммы квадратов его координат. Итак, имеем, что расстояние между двумя заданными точками М₁ и М₂ находится по формуле: ,.

Пусть теперь известно, что точка М делит отрезок М₁М₂ в отношении λ;. Найти координаты точки М. Обозначим их через М(х,у,z). То, что точка М(х,у,z) делит отрезок в отношении , означает, что .

Координаты х, у, z точки М:

.

В частности, если точка М делит отрезок М₁М₂ пополам, то λ; =1

,

Пример 3.1. Заданны координаты двух точек М₁ (-3;0;1) и М₂(2;2;-3). Найти:

1) Расстояние между этими точками;

2) Координаты точки М, делящей отрезок М₁М₂ на две равные части.

Решение

Найдем расстояние между этими точками:

Найдем координаты точки : .

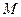- искомая точка.