Уравнение прямой, проходящей через данную точку перпендикулярно данному векторуНайдем уравнение прямой, проходящей через заданную точку Мо (хО; уо) перпендикулярно данному ненулевому вектор n = (А; В). Возьмем на прямой произвольную точку М(х; у) и рассмотрим вектор М0М (х — х0; у - уо) (см. рис.1). Поскольку векторы n и МоМ перпендикулярны, то их скалярное произведение равно нулю: то есть А(х — хо) + В(у — уо) = 0. (10.8) Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору. Вектор n= (А; В), перпендикулярный прямой, называется нормальным нормальным вектором этой прямой. Уравнение (10.8) можно переписать в виде Ах + Ву + С =0, (10.9) где А и В координаты нормального вектора, С = —Ахо - Вуо - свободный член. Уравнение (10.9) есть общее уравнение прямой (см. рис.2).
Рис.1 Рис.2 Канонические уравнения прямой
Где
Кривые второго порядка Окружность Окружностью называется множество всех точек плоскости, равноотстоящих от данной точки, которая называется центром. Каноническое уравнение круга радиуса R с центром в точке
В частности, если центр кола совпадает с началом координат, то уравнение будет иметь вид: Эллипс Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек
где a длина большой полуоси; b – длина малой полуоси (рис. 2). Зависимость между параметрами эллипса
Эксцентриситетом эллипса называется отношение межфокусного расстояния 2с к большой оси 2а: Директрисами эллипса называются прямые, параллельные оси Оу, которые находятся от этой оси на расстоянии Если в уравнении эллипса Итак,
|
,
- координаты точки, через которую проходит прямая, а 
- направляющий вектор.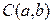
:
и 
, которые называются фокусами, есть величина постоянная 
, большая чем расстояние между фокусам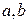и 
.
и 
выражается соотношением:
(4)
. Уравнения директрис: 
.
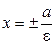, тогда фокусы эллипса находятся на оси Оу.
