Длина дуги плоской кривой
Примеры: Пример 1. Вычислить интегралы: а) Решение: а)
б) в) Пример 2. Исследовать на сходимость интеграл Решение:
Т.о., данный интеграл является сходящимся.
Пример 3. Найти площадь фигуры, ограниченной параболой Решение: Найдем точки пересечения прямой с параболой:
Ответ: Пример 4. Найти площадь плоской фигуры, ограниченной кардиоидой Решение
Пример 5. Вычислить объём тела, образованного вращением вокруг оси Ох косинусоиды в пределах от Решение: Объем тела вращения находим по формуле
Длина дуги плоской кривой, заданной параметрически вычисляется так:
Тогда
Пример 7. Вычислить с помощью формулы трапеций приближенное значение определенного интеграла Решение
Подынтегральная функция Используя данные, взятые из таблицы, приближенно вычислим интеграл: Ответ:
|
, от точки 
до 
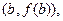то
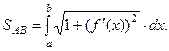
то точки А та В имеют координаты 
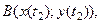то
и координаты точек А и В: 
то
б) 
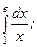в) 
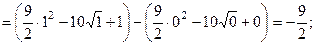
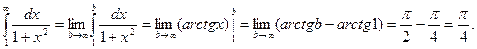
и прямой 
Искомую площадь найдем как разность двух площадей криволинейных трапеций: ограниченных прямой и параболой.
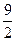(кв.ед.).
до 
.
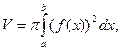где в нашем случае 
Пример 6. Вычислить длину одной арки циклоиды 
Найдем для нашего случая
при n = 10.
. Разобьем сегмент [0;1] на 10 частей, получим точки 
. Составим таблицу.
