Связь между определенным и неопределенным интегралом
При сравнении определенного и неопределенного интеграла видно, что это разные понятия: определенный интеграл - это число, а неопределенный интеграл - это функция. И все же между ними существует связь, которая разрешила найти удобный способ для вычисления определенного интеграла. Прежде чем сформулировать его, рассмотрим определенный интеграл с переменным верхним пределом. Таким образом, пусть в определенном интеграле
Используя свойства определенного интеграла 8.14 и 8.13 из формулы (8.15), получим
где По определению производной
Таким образом, мы выяснили, что Если
Итак, производная от определенного интеграла по переменной верхней границе равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхней границы. При
Сформулируем и докажем теперь теорему Ньютона - Лейбница. Теорема.4. Если
Эта формула и называется формулой Ньютона - Лейбница. Докажем ее. По условию теоремы
Предоставим
Отсюда, используя (8.9), имеем, что
С учетом (8.19) формула (8.18) примет вид
При
или, изменив обозначение переменной интегрирования на Введем обозначение
Формула (8.20) (Ньютона-Лейбница) дает практически удобный метод вычисления определенных интегралов в том случае, если известна первообразная для подынтегральной функции. С открытием этой формулы математика получила общий метод для решения разных задач, что позволило значительно расширить круг применений определенного интеграла. Итак, задача вычисления определенного интеграла свелась к последовательности двух задач: вычисления неопределенного интеграла (первообразной), а потом вычисления приращения первообразной на заданном промежутке. Для вычисления неопределенного интеграла применяются два основных метода: метод подстановки и интегрирования по частям. Рассмотрим некоторую специфику применения этих методов при вычислении определенного интеграла.
|

 нижняя граница постоянна и равна
нижняя граница постоянна и равна  , а верхняя граница изменяется, поэтому обозначим ее через х, а чтобы не путать с переменной интегрирования, обозначим последнюю через
, а верхняя граница изменяется, поэтому обозначим ее через х, а чтобы не путать с переменной интегрирования, обозначим последнюю через  . Пусть
. Пусть 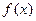 непрерывна на
непрерывна на 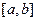 . Рассмотрим интеграл
. Рассмотрим интеграл  . Каждому значению переменной
. Каждому значению переменной  отвечает определенное значение интеграла. Итак,
отвечает определенное значение интеграла. Итак,  и найдем производную от этой функции по переменной
и найдем производную от этой функции по переменной 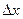 и вычислим приращение
и вычислим приращение 
 (8.15)
(8.15) ,
, находится между
находится между 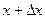 .
. .
. то есть мы доказали теорему:
то есть мы доказали теорему: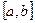 и
и  , то имеет место равенство
, то имеет место равенство (8.16)
(8.16) имеет геометрическое толкование - площадь криволинейной трапеции
имеет геометрическое толкование - площадь криволинейной трапеции 
 Из рис. 8.6 видно, что с изменением
Из рис. 8.6 видно, что с изменением  является функцией переменной
является функцией переменной 
 какая-то первообразная для непрерывной функции
какая-то первообразная для непрерывной функции  . (8.17)
. (8.17) является первообразной для
является первообразной для  является также первообразной для функции
является также первообразной для функции  Две первообразные для одной функции отличаются на постоянное слагаемое, значит,
Две первообразные для одной функции отличаются на постоянное слагаемое, значит, (8.18)
(8.18) , тогда
, тогда
 откуда
откуда (8.19)
(8.19)
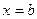 из этого имеем, что
из этого имеем, что
 , тогда формула (8.17) приобретает вид
, тогда формула (8.17) приобретает вид (8.20)
(8.20)


