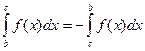Основные свойства определенного интеграла. Из формулы определенного интеграла и основных теорем о пределах вытекают следующие свойства определенного интеграла:
Из формулы определенного интеграла и основных теорем о пределах вытекают следующие свойства определенного интеграла: 1.Постоянный множитель можно выносить за знак определенного интеграла, то есть, если
2. Определенный интеграл от алгебраической суммы конечного количества непрерывных функций равен алгебраической сумме интегралов от каждого слагаемого, то есть
3. Если на отрезке
Если
Поскольку 4. Если
Для Для
Площадь криволинейной трапеции
5. (Теорема о среднем). Если функция
6. Для произвольных трех чисел
если только все эти три интеграла существуют. В случае, когда Если же
откуда имеем:
Учитывая замечание (2) о том, что (при изменении пределов интегрирования знак изменяется на противоположный), отсюда получим, что
|

 - постоянная, то
- постоянная, то (8.10.)
(8.10.) (8.11)
(8.11)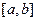 , где
, где  функции
функции 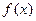 и
и  удовлетворяют условию
удовлетворяют условию 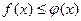 , то
, то
 и
и 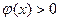 , то это свойство можно продемонстрировать геометрически (рис.8.2).
, то это свойство можно продемонстрировать геометрически (рис.8.2).
 ,
,  , это площадь криволинейной трапеции
, это площадь криволинейной трапеции  больше площади криволинейной трапеции
больше площади криволинейной трапеции  .
.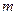 и
и  наименьшее и наибольшее значение функции
наименьшее и наибольшее значение функции  , то
, то (8.12)
(8.12) это свойство иллюстрируется геометрически таким образом (рис. 8.3):
это свойство иллюстрируется геометрически таким образом (рис. 8.3):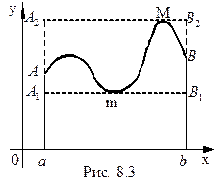
 больше площади прямоугольника
больше площади прямоугольника  , что будет справедливым равенство:
, что будет справедливым равенство: (8.13)
(8.13) Геометрически для случая, когда
Геометрически для случая, когда  , это означает (рис.8.4), что площадь под кривой
, это означает (рис.8.4), что площадь под кривой  и
и 
 справедливо равенство
справедливо равенство (8.14)
(8.14) содержится между
содержится между  и
и 
 і
і  , то
, то