Определенный интеграл является одним из основных понятий математического анализа и широко используется в разных областях науки, техники и в экономических исследованиях.
1. Задача вычисления площади криволинейной трапеции.
Пусть на отрезке [ a, b ] определена непрерывная функция у = f(х). Пусть f≥0 для  .
.
 Определение 1. Криволинейной трапецией называется фигура, ограниченная прямыми х = а и х = b, отрезком [ a, b ] оси Ох и кривой у = f(х) (рис. 1).
Определение 1. Криволинейной трапецией называется фигура, ограниченная прямыми х = а и х = b, отрезком [ a, b ] оси Ох и кривой у = f(х) (рис. 1).
Вычислим площадь этой криволинейной трапеции. С этой целью разобьем отрезок [ a, b ] произвольным образом на 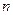 частей точками
частей точками 
 . Обозначим концы отрезка [ a, b ]
. Обозначим концы отрезка [ a, b ] 
 . Тогда отрезок [ a, b ] разобьется на
. Тогда отрезок [ a, b ] разобьется на 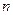 отрезков
отрезков
 .
.
Обозначим их длины через  . Через точки разбиения
. Через точки разбиения  проведем перпендикуляры к оси Ох и продолжим их к пересечению с кривой у = f(х). Эти перпендикуляры разделят площадь криволинейной трапеции на
проведем перпендикуляры к оси Ох и продолжим их к пересечению с кривой у = f(х). Эти перпендикуляры разделят площадь криволинейной трапеции на 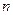 узких криволинейных трапеций. Заменим каждую из этих трапеций прямоугольником с основанием
узких криволинейных трапеций. Заменим каждую из этих трапеций прямоугольником с основанием  и высотой
и высотой  , где
, где  . Площадь каждого такого прямоугольника равна
. Площадь каждого такого прямоугольника равна  . Сумма площадей всех таких прямоугольников будет равна
. Сумма площадей всех таких прямоугольников будет равна
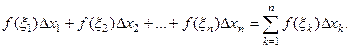
Таким образом, площадь S криволинейной трапеции приближенно равна этой сумме, то есть
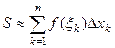 . (8.1)
. (8.1)
Эта формула будет тем точнее, чем меньше величина  .
.
Чтобы получить точную формулу для вычисления площади S криволинейной трапеции, надо в этой формуле перейти к пределу, когда  . Тогда
. Тогда
 . (8.2)
. (8.2)
Требование  обеспечивает равномерность разбиения отрезка [ a, b ] на части.
обеспечивает равномерность разбиения отрезка [ a, b ] на части.
Задача на вычисление пути, пройденного материальной точкой.
Пусть нужно определять путь  , который прошла материальная точка, движущаяся по прямой с переменной скоростью
, который прошла материальная точка, движущаяся по прямой с переменной скоростью  за время от
за время от  до
до 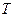 .
.
Поделим промежуток времени  на
на 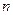 промежутков:
промежутков: 
 . Обозначим через
. Обозначим через  произвольный момент времени из промежутка
произвольный момент времени из промежутка  , а значения скорости в этой точке обозначим
, а значения скорости в этой точке обозначим 
 Точка, движущаяся с постоянной скоростью
Точка, движущаяся с постоянной скоростью 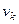 на промежутке
на промежутке  , проходит за это время путь
, проходит за это время путь  , а за время
, а за время  она пройдет путь
она пройдет путь
 .
.
Путь, который проходит точка за время  , вычисленный таким образом, будет отличаться от настоящего пути, но тем меньшее, чем меньше будет промежуток времени
, вычисленный таким образом, будет отличаться от настоящего пути, но тем меньшее, чем меньше будет промежуток времени  , тем меньшее изменяется скорость движения. Итак, когда
, тем меньшее изменяется скорость движения. Итак, когда  , тогда переменная скорость на промежутке
, тогда переменная скорость на промежутке  мало отличается от постоянной
мало отличается от постоянной 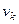 . Поэтому соответствующее действительности значение пути, пройденного точкой за время
. Поэтому соответствующее действительности значение пути, пройденного точкой за время  , будет равно пределу этой суммы при
, будет равно пределу этой суммы при  , т.е.
, т.е.
 . (8.3)
. (8.3)
3. Задача о работе переменной силы.
Пусть материальная точка  , двигаясь прямолинейно под действием силы
, двигаясь прямолинейно под действием силы  прошла путь
прошла путь  от точки
от точки  до точки
до точки  в направления действия этой силы. Надо вычислить работу
в направления действия этой силы. Надо вычислить работу  , силы
, силы 
Если сила  во время прямолинейного движения точки
во время прямолинейного движения точки  сохраняла постоянное значение, то искомая работа
сохраняла постоянное значение, то искомая работа
 .
.
Пусть теперь сила  изменяется во время движения точки М, т.е. является функцией абсциссы точки М в системе координат, введенной таким образом, положительное направление оси
изменяется во время движения точки М, т.е. является функцией абсциссы точки М в системе координат, введенной таким образом, положительное направление оси  совпадает с направлением движения точки М. Пусть абсциссы точек А и В соответственно
совпадает с направлением движения точки М. Пусть абсциссы точек А и В соответственно  и
и  , т.о.
, т.о.  .
.
Разобьем отрезок 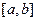 произвольным чином на
произвольным чином на 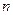 отрезков
отрезков 
 где
где 

 - абсциссы точек распределения. Обозначим длины этих отрезков через
- абсциссы точек распределения. Обозначим длины этих отрезков через  .
.
Будем считать, что на каждом частичном отрезке сила  сохраняет постоянное значение, которое она имеет в начале каждого отрезка:
сохраняет постоянное значение, которое она имеет в начале каждого отрезка:  , тогда работа по перемещению материальной точки на каждом из отрезков будет равняться соответственно
, тогда работа по перемещению материальной точки на каждом из отрезков будет равняться соответственно  ,
,
а вся работа приближенно определится как сумма 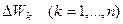
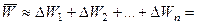
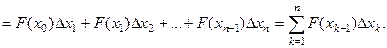
 - дает приближенное значение работы, произведенной силой
- дает приближенное значение работы, произведенной силой  при перемещении материальной точки на пути АВ.
при перемещении материальной точки на пути АВ.
 будет тем меньшее отличаться от
будет тем меньшее отличаться от  , чем меньшими будут частичные отрезки
, чем меньшими будут частичные отрезки  так как чем меньшее
так как чем меньшее  , тем меньшее успевает измениться значения силы
, тем меньшее успевает измениться значения силы  на этом промежутке. Поэтому точное значение работы
на этом промежутке. Поэтому точное значение работы  ми найдем, если перейдем к пределу суммы
ми найдем, если перейдем к пределу суммы  при условии, что длины частичных отрезков направляются к нулю. Итак, имеем
при условии, что длины частичных отрезков направляются к нулю. Итак, имеем
 . (8.4)
. (8.4)
Рассмотрев три разных задачи, мы видим, что с математической точки зрения их решения, которые даются формулами (8.2-8.4), отображают одинаковую задачу.
Определенный интеграл и его содержание
Пусть функция 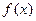 задана на отрезке
задана на отрезке 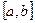 . Сделаем следующие шаги:
. Сделаем следующие шаги:
1) разобьем отрезок 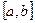 произвольным образом на
произвольным образом на 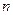 отрезков точками
отрезков точками  ;
;
2) на каждом отрезке  длиной
длиной  выберем произвольную точку
выберем произвольную точку  ;
;
3) вычислим значение функции в этой точке  где
где  ;
;
4) найдем сумму
 (8.5)
(8.5)
Ее называют интегральной суммой для функции 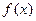 на отрезке
на отрезке 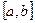 .
.
5) вычислим предел интегральной суммы при условии, что максимальная из длин частичных отрезков  стремится к нулю. Если этот предел существует, конечен, не зависит от способа разбиения отрезка
стремится к нулю. Если этот предел существует, конечен, не зависит от способа разбиения отрезка 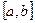 , и от способа выбора точки
, и от способа выбора точки  на каждом из частичных отрезков, то она и называется определенным интегралом от функции
на каждом из частичных отрезков, то она и называется определенным интегралом от функции 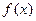 на отрезке
на отрезке 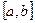 . Т.о.:
. Т.о.:
Определение.2. Если существует конечный предел интегральной суммы (8.5) при  , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка 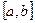 на
на 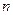 частичных отрезков и выбора точек
частичных отрезков и выбора точек  на каждом из них, то этот предел называется определенным интегралом от функции
на каждом из них, то этот предел называется определенным интегралом от функции 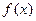 на отрезке
на отрезке 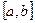 и обозначается
и обозначается
 .
.
Функция 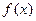 называется в этом случае интегральной на отрезке
называется в этом случае интегральной на отрезке 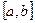 .
.
Итак, математически это определение можно записать так:
 (8.6)
(8.6)
Числа  и
и  называют нижним и верхним пределами интегрирования соответственно,
называют нижним и верхним пределами интегрирования соответственно, 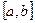 - отрезок интегрирования,
- отрезок интегрирования,  - переменная интегрирования.
- переменная интегрирования.
В соответствии с этим определением равенства (8.2)-(8.4) теперь можно записать в виде  (8.7)
(8.7)
то есть площадь криволинейной трапеции  , путь
, путь  , пройденный точкой с переменной скоростью
, пройденный точкой с переменной скоростью  , работа по перемещению материальной точки под действием переменной силы
, работа по перемещению материальной точки под действием переменной силы  выражаются определенным интегралом.
выражаются определенным интегралом.
Из определение (8.2) не вытекает, что любая функция интегрируема на любом отрезке. Можно найти такие функции, для которых определенный интеграл не существует, то есть интегральная сумма не стремится к какому-либо конечному пределу. Поэтому отметим условия, при которых функция является интегрируемой.
Теорема.1. Если функция  непрерывна на отрезке
непрерывна на отрезке 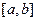 , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
Теорема 2. Если функция  на отрезке
на отрезке 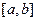 ограничена и имеет конечное количество точек разрыва, то она интегрируема на отрезке
ограничена и имеет конечное количество точек разрыва, то она интегрируема на отрезке 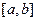 .
.
Теорема 3. Монотонная ограниченная функция 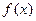 всегда интегрируема.
всегда интегрируема.
Замечание 1. Отметим, что определенный интеграл зависит только от вида функции  и пределов интегрирования, но не зависит от обозначения переменной интегрирования, то есть
и пределов интегрирования, но не зависит от обозначения переменной интегрирования, то есть
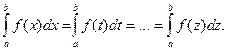
Замечание 2. При введении понятия определенного интеграла  мы предполагали, что
мы предполагали, что  . Если
. Если  , то примем по определению
, то примем по определению
 (8.8)
(8.8)
Замечание 3. В случае  будем считать по определению
будем считать по определению
 (8.9)
(8.9)
Замечание 4. Вычисление  по определению, то есть как предела интегральной суммы, связано с большой вычислительной трудностью, поэтому возникает задача: найти практически удобный метод его вычисления. Этот метод мы рассмотрим дальше.
по определению, то есть как предела интегральной суммы, связано с большой вычислительной трудностью, поэтому возникает задача: найти практически удобный метод его вычисления. Этот метод мы рассмотрим дальше.

 .
. Определение 1. Криволинейной трапецией называется фигура, ограниченная прямыми х = а и х = b, отрезком [ a, b ] оси Ох и кривой у = f(х) (рис. 1).
Определение 1. Криволинейной трапецией называется фигура, ограниченная прямыми х = а и х = b, отрезком [ a, b ] оси Ох и кривой у = f(х) (рис. 1).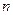 частей точками
частей точками 
 . Обозначим концы отрезка [ a, b ]
. Обозначим концы отрезка [ a, b ] 
 . Тогда отрезок [ a, b ] разобьется на
. Тогда отрезок [ a, b ] разобьется на  .
. . Через точки разбиения
. Через точки разбиения  проведем перпендикуляры к оси Ох и продолжим их к пересечению с кривой у = f(х). Эти перпендикуляры разделят площадь криволинейной трапеции на
проведем перпендикуляры к оси Ох и продолжим их к пересечению с кривой у = f(х). Эти перпендикуляры разделят площадь криволинейной трапеции на  и высотой
и высотой  , где
, где  . Площадь каждого такого прямоугольника равна
. Площадь каждого такого прямоугольника равна  . Сумма площадей всех таких прямоугольников будет равна
. Сумма площадей всех таких прямоугольников будет равна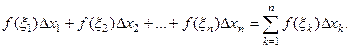
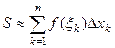 . (8.1)
. (8.1) . Тогда
. Тогда . (8.2)
. (8.2) обеспечивает равномерность разбиения отрезка [ a, b ] на части.
обеспечивает равномерность разбиения отрезка [ a, b ] на части. , который прошла материальная точка, движущаяся по прямой с переменной скоростью
, который прошла материальная точка, движущаяся по прямой с переменной скоростью  за время от
за время от  до
до 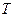 .
. на
на 
 . Обозначим через
. Обозначим через  произвольный момент времени из промежутка
произвольный момент времени из промежутка  , а значения скорости в этой точке обозначим
, а значения скорости в этой точке обозначим 
 Точка, движущаяся с постоянной скоростью
Точка, движущаяся с постоянной скоростью 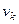 на промежутке
на промежутке  , а за время
, а за время  .
. , тогда переменная скорость на промежутке
, тогда переменная скорость на промежутке  , т.е.
, т.е. . (8.3)
. (8.3) , двигаясь прямолинейно под действием силы
, двигаясь прямолинейно под действием силы  прошла путь
прошла путь  до точки
до точки  в направления действия этой силы. Надо вычислить работу
в направления действия этой силы. Надо вычислить работу  , силы
, силы 
 .
. совпадает с направлением движения точки М. Пусть абсциссы точек А и В соответственно
совпадает с направлением движения точки М. Пусть абсциссы точек А и В соответственно  и
и  , т.о.
, т.о.  .
.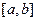 произвольным чином на
произвольным чином на 
 где
где 

 - абсциссы точек распределения. Обозначим длины этих отрезков через
- абсциссы точек распределения. Обозначим длины этих отрезков через  .
. , тогда работа по перемещению материальной точки на каждом из отрезков будет равняться соответственно
, тогда работа по перемещению материальной точки на каждом из отрезков будет равняться соответственно  ,
,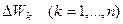
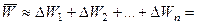
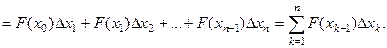
 - дает приближенное значение работы, произведенной силой
- дает приближенное значение работы, произведенной силой  так как чем меньшее
так как чем меньшее  , тем меньшее успевает измениться значения силы
, тем меньшее успевает измениться значения силы  на этом промежутке. Поэтому точное значение работы
на этом промежутке. Поэтому точное значение работы  при условии, что длины частичных отрезков направляются к нулю. Итак, имеем
при условии, что длины частичных отрезков направляются к нулю. Итак, имеем . (8.4)
. (8.4)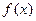 задана на отрезке
задана на отрезке 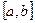 . Сделаем следующие шаги:
. Сделаем следующие шаги: ;
; длиной
длиной  выберем произвольную точку
выберем произвольную точку  ;
; где
где  ;
; (8.5)
(8.5) на каждом из частичных отрезков, то она и называется определенным интегралом от функции
на каждом из частичных отрезков, то она и называется определенным интегралом от функции  , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка  .
. (8.6)
(8.6) - переменная интегрирования.
- переменная интегрирования. (8.7)
(8.7) , работа по перемещению материальной точки под действием переменной силы
, работа по перемещению материальной точки под действием переменной силы  непрерывна на отрезке
непрерывна на отрезке  и пределов интегрирования, но не зависит от обозначения переменной интегрирования, то есть
и пределов интегрирования, но не зависит от обозначения переменной интегрирования, то есть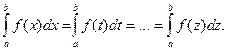
 . Если
. Если  , то примем по определению
, то примем по определению (8.8)
(8.8) будем считать по определению
будем считать по определению (8.9)
(8.9) по определению, то есть как предела интегральной суммы, связано с большой вычислительной трудностью, поэтому возникает задача: найти практически удобный метод его вычисления. Этот метод мы рассмотрим дальше.
по определению, то есть как предела интегральной суммы, связано с большой вычислительной трудностью, поэтому возникает задача: найти практически удобный метод его вычисления. Этот метод мы рассмотрим дальше.


