Интегрирование подстановкой
Пусть надо вычислить определенный интеграл где Если при этом будут выполняться такие условия: 1) при изменении
2) сложная функция
Формула (8.25) и выражает собою суть метода подстановки. Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к старой переменной (как это нужно было делать при вычислении неопределенного интеграла) достаточно лишь учесть границы интегрирования соответственно (8.24). Пример 8.3. Вычислить Решение Введем новую переменную
из которой видно, что при
Пример 4. Вычислить Решение. Произведем замену переменной: при Итак, получаем
Таким образом, видим, что различие в применении метода замены переменной в неопределенном и определенном интеграле состоит в том, что в втором случае не надо возвращаться к старой переменной, поскольку при замене переменной изменяются также и границы интегрирования.
|
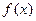- непрерывная на 
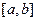функция, а первообразной для нее нет в таблице простейших интегралов. Тогда произведем замену переменной, а именно, введем новую переменную 
таким образом: 
, где 
- непрерывно дифференцируема на 
функция.
до 
переменная 
изменяется от 
до 
, то есть
. (8.24)
определена и непрерывна на отрезке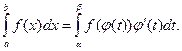 
(8.25)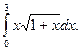
. Тогда 
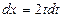. Вычислим границы интегрирования и результат представим в виде табл. 1. Таблица 1
, а при 
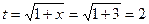. Итак, после введении новой переменной получим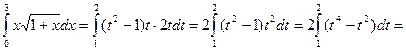
.
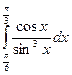. Тогда 
, а границы интегрирования приобретают значения: при 
