Пусть надо вычислить 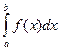 , но первообразная для функции
, но первообразная для функции 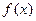 не выражается через элементарные функции. Тогда применить формулу Ньютона-Лейбница невозможно. В таких случаях применяются методы приближенного вычисления определенных интегралов. Рассмотрим их, используя определение интеграла как границы интегральной суммы. Разделим отрезок
не выражается через элементарные функции. Тогда применить формулу Ньютона-Лейбница невозможно. В таких случаях применяются методы приближенного вычисления определенных интегралов. Рассмотрим их, используя определение интеграла как границы интегральной суммы. Разделим отрезок 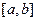 точками
точками 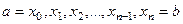 на
на 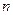 частичных отрезков равной длины. Обозначим длину каждый из них через
частичных отрезков равной длины. Обозначим длину каждый из них через 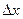 . Тогда
. Тогда
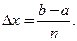
Обозначим через 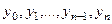 значения функции
значения функции 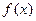 в точках
в точках 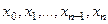 , то есть
, то есть
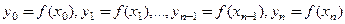 .
.
Составим суммы:
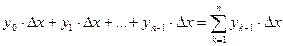 ,
,
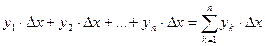 .
.
Каждая из этих сумм представляет собой интегральную сумму для 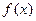 на отрезке
на отрезке 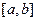 и поэтому приближенно выражает интеграл
и поэтому приближенно выражает интеграл
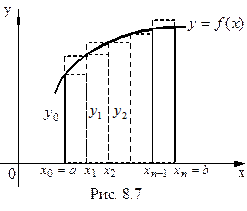
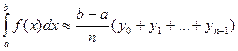 , (8.26)
, (8.26)
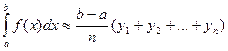 . (8.27)
. (8.27)
Из рис. 8.7 видно, что формула (8.26) выражает площадь ступенчатой фигуры, составленной из прямоугольников, вписанных в криволинейную трапецию, а формула (8.27) выражает площадь ступенчатой фигуры, составленной из прямоугольников, описанных вокруг криволинейной трапеции. Поэтому формулы (8.26; 8.27) называются формулами прямоугольников. Погрешность при вычислении интегралов за формулами прямоугольников будет тем меньше, чем больше число n. Она выражается формулой 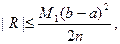
где 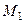 - максимальное значение абсолютной величины производной
- максимальное значение абсолютной величины производной 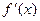 на
на 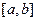 .
.
Более точное значение определенного интеграла получим, если данную кривую заменим не ступенчатой линией, как это делается в формуле прямоугольников, а вписанной ломаной (рис. 8.8).
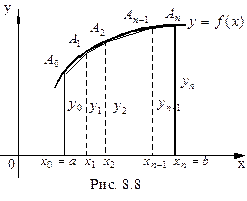 Тогда площадь криволинейной трапеции
Тогда площадь криволинейной трапеции 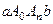 заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами
заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами 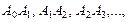
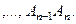 Поскольку площадь первой из этих трапеций равна
Поскольку площадь первой из этих трапеций равна  , площадь второй равняется
, площадь второй равняется 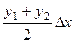 , то
, то
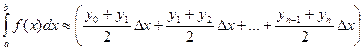
или
 . (8.28)
. (8.28)
Легко видеть, что она дает среднее арифметическое из формул (8.26 и 8.27). Формула (8.28) называется формулой трапеций. В этом случае погрешность вычисляется по формуле 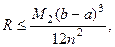
где 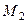 - минимальное значение абсолютной величины второй производной
- минимальное значение абсолютной величины второй производной 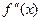 на
на 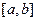 .
.
Более точные результаты можно получить по формуле Симпсона (или формуле парабол), которая имеет вид:
 (8.29)
(8.29)
При этому надо обратить внимание на то, что число 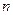 частичных отрезков, на которые разбивается отрезок
частичных отрезков, на которые разбивается отрезок 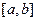 , должно быть обязательно четным, то есть
, должно быть обязательно четным, то есть 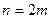 . Тогда каждые две соседних криволинейных трапеции, на которые разбилась вся криволинейная трапеция
. Тогда каждые две соседних криволинейных трапеции, на которые разбилась вся криволинейная трапеция 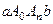 (рис. 8.8), заменяются параболической трапецией, площадь которой исчисляется по формуле
(рис. 8.8), заменяются параболической трапецией, площадь которой исчисляется по формуле 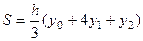 ,
,
 где
где 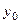 и
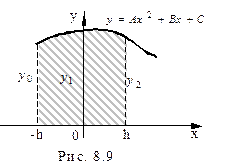
и 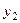 - крайние ординаты,
- крайние ординаты, 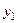 - ордината кривой в середине отрезка, а
- ордината кривой в середине отрезка, а 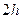 - расстояние между ординатами
- расстояние между ординатами 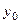 и
и 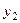 (рис. 8.9).
(рис. 8.9).
Погрешность при этом может быть вычислена по формуле
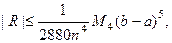
где 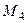 - максимальное значение абсолютной величины производной
- максимальное значение абсолютной величины производной 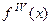 на отрезке
на отрезке 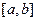 .
.
Пример.5. Вычислить приближенно 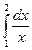 .
.
Точное значение его 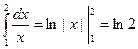 . З точностью до седьмого знака
. З точностью до седьмого знака 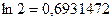 . Вычислим теперь его значение, пользуясь формулами (8.26-8.29). Для этого разделим отрезок
. Вычислим теперь его значение, пользуясь формулами (8.26-8.29). Для этого разделим отрезок 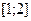 на 10 равных отрезков. Тогда длина каждого из них будет
на 10 равных отрезков. Тогда длина каждого из них будет 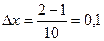 .
.
Составим табл. 2 значений подынтегральной функции в точках разбиения  .
.
Таблица 2
Тогда по формуле (8.26) получим 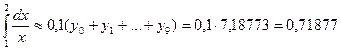 .
.
По формуле (8.27) 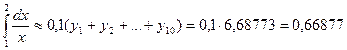 .
.
По формуле (8.28)  .
.
По формуле Симпсона (8.29)
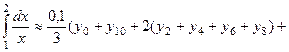
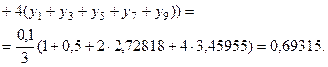
Таким образом, по формуле Симпсона при  получили 5 верных знаков, по формуле трапеций - лишь три верных знака, за формулами прямоугольников мы можем быть уверены только в одном знаке.
получили 5 верных знаков, по формуле трапеций - лишь три верных знака, за формулами прямоугольников мы можем быть уверены только в одном знаке.

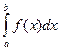 , но первообразная для функции
, но первообразная для функции 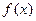 не выражается через элементарные функции. Тогда применить формулу Ньютона-Лейбница невозможно. В таких случаях применяются методы приближенного вычисления определенных интегралов. Рассмотрим их, используя определение интеграла как границы интегральной суммы. Разделим отрезок
не выражается через элементарные функции. Тогда применить формулу Ньютона-Лейбница невозможно. В таких случаях применяются методы приближенного вычисления определенных интегралов. Рассмотрим их, используя определение интеграла как границы интегральной суммы. Разделим отрезок 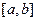 точками
точками 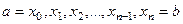 на
на 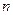 частичных отрезков равной длины. Обозначим длину каждый из них через
частичных отрезков равной длины. Обозначим длину каждый из них через 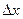 . Тогда
. Тогда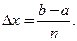
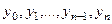 значения функции
значения функции 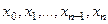 , то есть
, то есть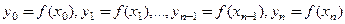 .
.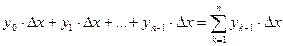 ,
,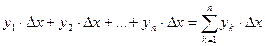 .
.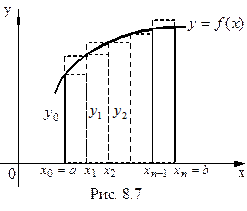
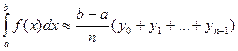 , (8.26)
, (8.26)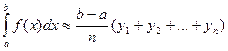 . (8.27)
. (8.27)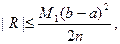
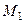 - максимальное значение абсолютной величины производной
- максимальное значение абсолютной величины производной  на
на 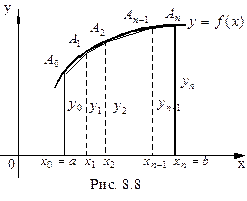 Тогда площадь криволинейной трапеции
Тогда площадь криволинейной трапеции 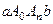 заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами
заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами 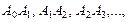
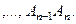 Поскольку площадь первой из этих трапеций равна
Поскольку площадь первой из этих трапеций равна  , площадь второй равняется
, площадь второй равняется 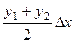 , то
, то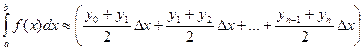
 . (8.28)
. (8.28)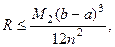
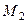 - минимальное значение абсолютной величины второй производной
- минимальное значение абсолютной величины второй производной 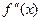 на
на  (8.29)
(8.29)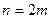 . Тогда каждые две соседних криволинейных трапеции, на которые разбилась вся криволинейная трапеция
. Тогда каждые две соседних криволинейных трапеции, на которые разбилась вся криволинейная трапеция 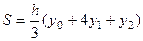 ,
, где
где 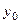 и
и 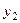 - крайние ординаты,
- крайние ординаты, 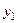 - ордината кривой в середине отрезка, а
- ордината кривой в середине отрезка, а 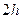 - расстояние между ординатами
- расстояние между ординатами 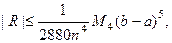
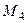 - максимальное значение абсолютной величины производной
- максимальное значение абсолютной величины производной 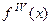 на отрезке
на отрезке 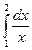 .
.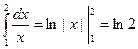 . З точностью до седьмого знака
. З точностью до седьмого знака 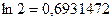 . Вычислим теперь его значение, пользуясь формулами (8.26-8.29). Для этого разделим отрезок
. Вычислим теперь его значение, пользуясь формулами (8.26-8.29). Для этого разделим отрезок 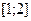 на 10 равных отрезков. Тогда длина каждого из них будет
на 10 равных отрезков. Тогда длина каждого из них будет 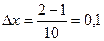 .
. .
.
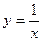
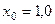
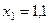
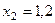
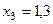
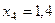
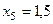
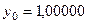

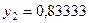
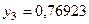
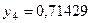
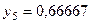
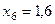

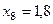
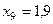
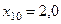
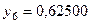
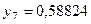
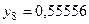

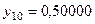
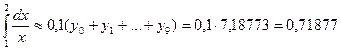 .
.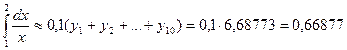 .
. .
.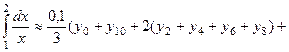
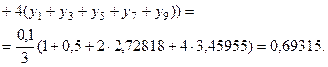
 получили 5 верных знаков, по формуле трапеций - лишь три верных знака, за формулами прямоугольников мы можем быть уверены только в одном знаке.
получили 5 верных знаков, по формуле трапеций - лишь три верных знака, за формулами прямоугольников мы можем быть уверены только в одном знаке.


