Answer: B.
5. Conversion of sinusoid v(t)= - 20sin100t in rectangular form gives us A. 10 – j17.3 B. 20 – j17.3 C. 0 + j20 D. 20 + j17.3 E. 10 – j15.3 Solution: v(t)= – 20sin100t = – 20cos(100t – 90°) 1st way: we rotate vector of length 20 by –90 from starting point on 180 degrees on 90° clockwise. We get vector of length 20 on imaginary axis.
2nd way: V = –20∟–90° V= –20cos(–90) –j20sin(–90)=0–j20(–1)=0+j20. Answer: C.
6. Conversion of phasor 169∟- 45° at f=60Hz to sinusoid gives us A. 169cos(150t-45°) B. 169cos(377t-45°) C. 169cos(377t+45°) D. 169cos(233t-45°) E. 169cos(155t-45°) Solution: ω=2πf=2*3.14*60=377 169∟- 45° = 169cos(377t-45°) Answer: B.
7. Convert the complex number (-12+j16) to polar form A. 18∟-126.8° B. 20∟126.8° C. 20∟-126.8° D. 22∟-56.8° E. 32∟56.8°
Solution:
V =20∟126.8° Answer: B. 8. Convert the complex number 100∟-120° to rectangular form. A. 50- j86.6 B. -50-j86.6 C. –50+j86.6 D.33-j75 E. –33-j75
Solution: VA=100. v(t)=100cos(ωt - 120°) V = 100cos(-120°) + j100sin(- 120)= -50-j86.6 Answer: B. 9. Complex number is 20+j11. What quadrant is the phase in? A. 1 B. 2 C.3 D.4 E.1 or 2
Solution:
Answer: A.
10. Convert the complex number 100∟-120° to rectangular form. A. 50- j86.6 B. -50-j86.6 C. –50+j86.6 D.33-j75 E. –33-j75
Solution: VA=100. v(t)=100cos(ωt - 120°) V = 100cos(-120°) + j100sin(- 120)= -50-j86.6 Answer: B.
11. Cyclic frequency for the function v(t)= 5cos(1000t+30°) is equal to A.1000 Hz B.100Hz C.500Hz D. 318Hz E.159.2Hz
Solution: ω=2πf; f=ω/2π = 1000/2π = 159.2Hz Answer: E. 12. Cyclic frequency f is equal to A. 2πT B. 1/2πT C. ω/2π; D. 2πω E. 2π/ω;
Solution: Angular frequency: ω=2πf; Cyclic frequency: f= ω/2π; Answer: C. 13. Define VA for the circuit in Fig.3. VA= A.VS*R4/(R1+R4) B. VS*R2/(R1+R4) C. VS*R3/(R1+R4) D. VS*R3/(R1+R3) E. VS*R4/(R1+R3)
By Voltage Division Rule:
|



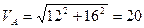
 Vector is situated in the second quadrant.
Vector is situated in the second quadrant.
 Solution:
Solution:



